Tìm giá trị nhỏ nhất của đa thức sau:
x2 + y2 - xy - 3x - 3y + 2021
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2021
\(A=x^2+y^2+z^2-yz-4x-3y+2027\)
\(\Rightarrow4A=4x^2+4y^2+4z^2-4yz-16x-12y+8108=4x^2-16x+16+3y^2+12y+12+y^2-4yz+4z^2+8080=4\left(x-2\right)^2+3\left(y+2\right)^2+\left(y-2z\right)^2+8080\)
Vì \(4\left(x-2\right)^2\ge0\)
\(3\left(y+2\right)^2\ge0\)
\(\left(y-2z\right)^2\ge0\)
\(\Rightarrow4A\ge8080\Rightarrow A\ge2020\)
\(ĐTXR\Leftrightarrow x=2,y=-2,z=-1\)
NN
0
CM
27 tháng 3 2017
a) Từ M = x − 3 2 2 + 31 4 ≥ 31 4 ⇒ M min = 31 4 ⇔ x = 3 2 .
b) Ta có N = ( x + 2 y ) 2 + ( y – 2 ) 2 + ( x + 4 ) 2 – 120 ≥ - 120 .
Tìm được N min = -120 Û x = -4 và y = 2.
PT
1
CM
4 tháng 12 2018
Ta có: M = x 2 + y 2 – x + 6y + 10 = ( y 2 + 6y + 9) + ( x 2 – x + 1)
= y + 3 2 + ( x 2 – 2.1/2 x + 1/4) + 3/4 = y + 3 2 + x - 1 / 2 2 + 3/4
Vì y + 3 2 ≥ 0 và x - 1 / 2 2 ≥ 0 nên y + 3 2 + x - 1 / 2 2 ≥ 0
⇒ M = y + 3 2 + x - 1 / 2 2 + 3/4 ≥ 3/4
⇒ M = 3/4 khi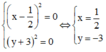 
Vậy M = 3/4 là giá trị nhỏ nhất tại y = -3 và x = 1/2
27 tháng 12 2021
Bài 1:
\(A=x^2+6x+9+x^2-10x+25\)
\(=2x^2+4x+34\)
\(=2\left(x^2+2x+17\right)\)
\(=2\left(x+1\right)^2+32>=32\forall x\)
Dấu '=' xảy ra khi x=-1
Đặt \(A = x^2 + y^2 - xy - 3x - 3y + 2021\)
\(\Rightarrow2A=2x^2+2y^2-2xy-6x-6y+4042\)
\(=\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+\left(y^2-6y+9\right)+4024\)
\(=\left(x-y\right)^2+\left(x-3\right)^2+\left(y-3\right)^2+4024\)
Mà \(\left(x-y\right)^2,\left(x-3\right)^2,\left(y-3\right)^2\ge0\)
\(\Rightarrow2A\ge4024\Leftrightarrow A\ge2012\)
Vậy GTNN của A là 2012 khi x = y = 3
Đặt A= x2 + y2 - xy -3x -3y + 2021
=> 2A= 2x2 +2y2 -2xy - 6x -6y + 4024
=> 2A= (x2 -2xy +y2) +( x2 - 6x +9) +(y2 -6y +9) + 4006
=> 2A= (x-y)2 +(x -3)2 +(y- 3)2 +4006
vì (x-y)2 + (x -3)2 + (y -3)2 \(\ge\) 0 với mọi x,y
=> 2A\(\ge\)4006 => A\(\ge\)2003
Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}x-y=0\Rightarrow x=y\\x-3=0\Rightarrow x=3\\y-3=0\Rightarrow y=3\end{matrix}\right.\) Vậy GTNN cửa A= 2003 khi x=y=3