cho hình vuông ABCD . Lấy điểm M trên BC ( khác B , C) tian p/g góc ADM cắt cạnh AB tại N. Cm DM=AN+CM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
KV
10 tháng 1
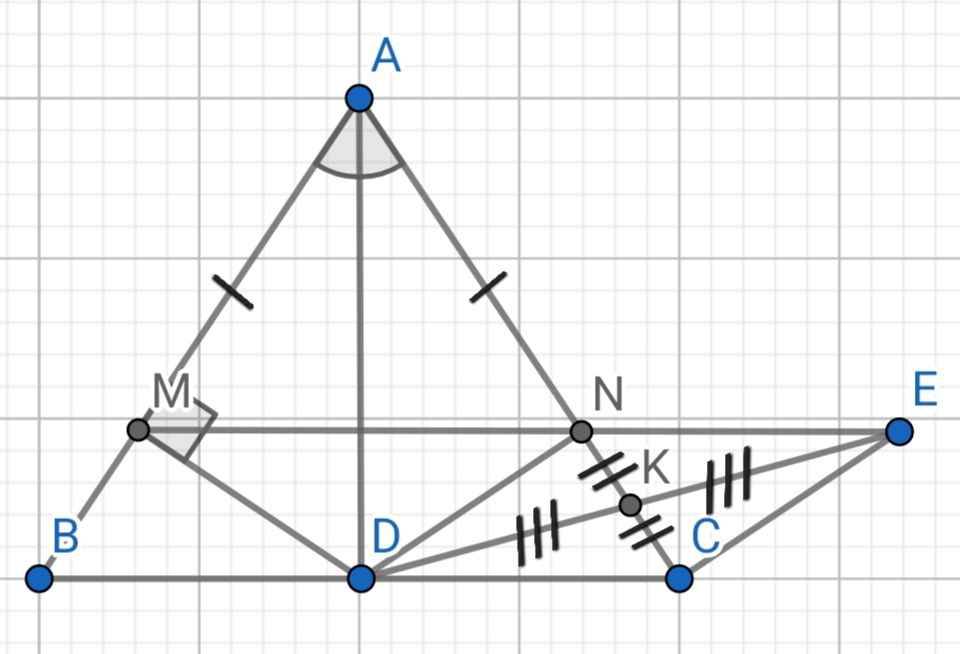a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng
11 tháng 10 2023
a: XétΔMAD vuông tại A và ΔNBA vuông tại B có
MA=NB
AD=BA
Do đó: ΔMAD=ΔNBA
=>DM=AN và \(\widehat{AMD}=\widehat{BNA}\)
=>\(\widehat{AMD}+\widehat{MAN}=90^0\)
=>DM vuông góc AN
b: AM+MB=AB
BN+NC=BC
mà AM=BN và AB=BC
nên MB=NC
Xét ΔMBC vuông tại B và ΔNCD vuông tại C có
MB=NC
BC=CD
Do đó: ΔMBC=ΔNCD
=>\(\widehat{BMC}=\widehat{CND}\)
=>\(\widehat{CND}+\widehat{NCM}=90^0\)
=>DN vuông góc MC
Xét ΔDMN có
CM,NA là đường cao
CM cắt NA tại X
Do đó: X là trực tâm
=>DX vuông góc MN
B1
31 tháng 7 2017
làm tương tự
Cho hình vuông ABCD. Gọi O là giao điểm của hai đường chéo AC và BD, M là trung điểm của OB, N là trung điểm của CD.
a, Chứng minh: +góc AMN vuông.
+A, M, N, D cùng thuộc một đường tròn, xác định tâm của nó.
+ AN>MD
b, Trên AB, AD thứ tự lấy I, K sao AI=Ak. Kẻ AP vuông góc DI, cắt BC tại Q. Chứng minh 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn
Bài làm
Từ M hạ ME vuông góc AD,MF vuông góc DC (ME//AB, MF//BC) , nối MA và MN ta có DM = 3/4.DB => AE = CF = 1/4 AD ( AD = DC= AB = BC cạnh hình vuông)
ME = MF = 3/4.AB, NC = 1/2.DC và CF = 1/4 DC => NF = 1/4 DC
=> tam giác vuông AEM = tam giác vuông NFM ( hai cặp cạnh góc vuông bằng nhau đôi một)
=>góc AME = góc NMF mà góc NMF + góc EMN = 90 độ => góc AME + góc EMN = 90 độ
=> góc AMN = 90 độ (điều phải cm)
Gọi I là trung điểm AN, do tam giác ADN vuông tại D =>ID= IA = IN (trung tuyến thuộc cạnh huyền bằng 1/2 cạnh huyền) , tương tự có tam giác AMN vuông tại M => IM = IA = IN
=> 4 điểm A, D, N, M cách đều I => A, M, N, D cùng thuộc một đường tròn tâm là trung điểm I của đoạn AN
tam giác vuông cân DEM có DM^2 = 2.ME^2
tam giác vuông cân AMN có AN^2 = 2.MA^2 mà MA > ME
=> AN^2 > DM^2 => AN > DM (điều phải cm)
b, Trên AB, AD thứ tự lấy I, K sao AI=Ak. Kẻ AP vuông góc DI, cắt BC tại Q. Chứng minh 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn
góc DPQ = 90 độ (theo cách dựng AP vuông góc DI)
và góc DCQ = 90 độ (gt ABCD là hình vuông) nên D, P, C, Q thuộc đường tròn đường kính DQ.
ta sẽ c/m K thuộc đường tròn đường kính DQ.nghĩa là góc DKQ = 90 độ
xét tứ giác IPQB có góc P và B vuông => góc PQB + góc PIB = 180 độ
mà góc góc PIB + góc PIA = 180 độ =>góc PIA =góc PQB => góc DIA = góc AQB
xét 2 tam giác vuông DAI và ABQ có AD = AB và góc DIA = góc AQB
=> tam giác DAI = tam giác ABQ ( cạnh góc vuông, góc nhọn) => AK = BQ => KQ//AB
=> góc DKQ = 90 độ => K thuộc đường tròn đường kính DQ.
=> 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn ( điều phải c/m)
1 tháng 4 2023
AH vuông góc DM
=>góc MAH=góc MDA
Xét ΔABP vuông tại B và ΔDAM vuông tại A có
AB=AD
góc MAH=góc MDA
=>ΔABP=ΔDAM
=>BP=AM=AN
mà BC=AD
nên PC=ND
=>PCND là hình chữ nhật
=>P,C,D,N cùng nằm trên đường tròn đường kính DP
mà H nằm trên đường tròn đường kính DP(góc DHP=90 độ)
nên C,D,N,H,P cùng thuộc 1 đường tròn