Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : \(a=6.k_1;b=6.k_2\)
Trong đó : \(ƯCLN\left(k_1,k_2\right)=1\)
Mà : \(a+b=84\Rightarrow6.k_1+6.k_2=84\)
\(\Rightarrow6\left(k_1+k_2\right)=84\Rightarrow k_1+k_2=84\div6=14\)
+) Nếu : \(k_1=1\Rightarrow k_2=13\Rightarrow\begin{cases}a=6\\b=78\end{cases}\)
+)Nếu : \(k_1=3\Rightarrow k_2=11\Rightarrow\begin{cases}a=18\\b=66\end{cases}\)
+)Nếu : \(k_1=5\Rightarrow k_2=9\Rightarrow\begin{cases}a=30\\b=54\end{cases}\)
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : \(ƯCLN\left(a,b\right)=10;BCNN\left(a,b\right)=900\)
\(\RightarrowƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b=900.10=9000\)
Phần còn lại giống câu a và câu b tự làm
a) n=7k+1 ( \(k\in N\))
b) 18 va 66 hoac 6 va 78 hoac 30 va 54
c) 15 va 20 hoac 5 va 60
d) 10 va 900 hoac 20 va 450 hoac 180 va 50 hoac 100 va 90
a, Gọi hai số phải tìm là a,b. Ta có (a;b) = 6 => a = 6a’, b = 6b’ với (a’,b’) = 1(a,b,a’,b’ ∈ N)
Do đó: a+b = 84 => 6.(a’+b’) = 84 => a’+b’ = 14
Chọn cặp số a’,b’ là hai số nguyên tố cùng nhau có tổng bằng 14 ta được:
Do đó:
b, Gọi hai số phải tìm là a.b. Ta có (a;b) = 5 => a = 5a’, b = 5b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N)
Do ab = 300 => 25a’b’ = 300 => a’b’ = 12 = 4.3
Chọn cặp số a’,b’ nguyên tố cùng nhau có tích bằng 12 ta được:
a’ = 1, b’ = 12 => a = 5, b = 60
a’ = 3, b’ = 4 => a = 15, b = 20
c, Gọi hai số phải tìm là a,b. Ta có (a;b) = 10 => a = 10a’; b = 10b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N, a’<b’). Do đó: ab = 100a’b’ (1)
Mặt khác: ab = [a,b].(a,b) = 900.10 = 9000 (2)
a’ = 1, b’ = 90 => a = 10, b = 900
a’ = 2, b’ = 45 => a = 20, b = 450
a’ = 5, b’ = 18 => a = 50, b = 180
a’ = 9, b’ = 10 => a = 90, b = 100
a) goi hai so la a ; b va a >b
vi UCLN(a,b)=18=>a=18k ; b=18q (trong do UCLN (k,q)=1 va k>q)
=>a+b=162
18k+18q =162
18(k+q)=162
k+q=9
| ta co bang sau | |||||||||||||||||||||||
vay ........... | |||||||||||||||||||||||
21453
52542000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 | 542454550212.100000000000000000000000000000000000000000000000000000000000000000000000000000 |
a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : a=6.k1;b=6.k2a=6.k1;b=6.k2
Trong đó : ƯCLN(k1,k2)=1ƯCLN(k1,k2)=1
Mà : a+b=84⇒6.k1+6.k2=84a+b=84⇒6.k1+6.k2=84
⇒6(k1+k2)=84⇒k1+k2=84÷6=14⇒6(k1+k2)=84⇒k1+k2=84÷6=14
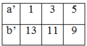
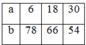
+) Nếu : k1=1⇒k2=13⇒{a=6b=78k1=1⇒k2=13⇒{a=6b=78
+)Nếu : k1=3⇒k2=11⇒{a=18b=66k1=3⇒k2=11⇒{a=18b=66
+)Nếu : k1=5⇒k2=9⇒{a=30b=54k1=5⇒k2=9⇒{a=30b=54
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : ƯCLN(a,b)=10;BCNN(a,b)=900ƯCLN(a,b)=10;BCNN(a,b)=900
⇒ƯCLN(a,b).BCNN(a,b)=a.b=900.10=9000⇒ƯCLN(a,b).BCNN(a,b)=a.b=900.10=9000
Phần còn lại giống câu a và câu b bạn tự làm nha
chúc bạn hok tốt