Cho hai đường thẳng (d1): y=12x+5-m; (d2): y=3x+3+m. Xác định m để giao điểm của (d1) và (d2) thỏa mãn
a) Nằm trên trục tung
b) Nằm bên trái trục tung
c) Nằm trong góc phần tư thứ hai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có phương trình hoành độ giao điểm của d 1 v à d 2 : m x – 2 = 1 2 x + 1 ( * )
Để hai đường thẳng d 1 v à d 2 cắt nhau tại một điểm có hoành độ x = − 4 t h ì x = − 4 thỏa mãn phương trình (*)
Suy ra m . ( − 4 ) – 2 = 1 2 . ( − 4 ) + 1 ⇔ − 4 m – 2 = − 2 + 1 ⇔ − 4 m = 1 ⇔ m = 1 4
Đáp án cần chọn là: A

a) Để d1 trùng d2 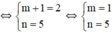
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 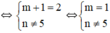
Vậy m = 1, n ≠ 5.

a) Để d1 trùng d2 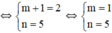
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 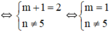
Vậy m = 1, n ≠ 5.

Gọi pt d2 có dạng \(y=ax+b\)
Do d2 qua A và B nên ta có:
\(\left\{{}\begin{matrix}a+b=2\\-3a+b=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\) \(\Rightarrow d_2:y=x+1\)
Do \(d_1\) song song \(d_2\) nên chúng có cùng hệ số góc
\(\Rightarrow k=1\)

Do đường thẳng d2 song song với d1 nên d2 có dạng : y = 1 2 x + b b ≠ - 2
Điểm A(2; 4) thuộc đường thẳng d2 nên: 4 = 1 2 . 2 + b ⇔ b = 3
Vậy phương trình đường thẳng d2: y = 1 2 x + 3
Chọn đáp án là C.

a.
Để hai đường thẳng song song:
\(\Rightarrow\left\{{}\begin{matrix}2m=-\dfrac{1}{3}\\m-1\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{1}{6}\\m\ne2\end{matrix}\right.\) \(\Leftrightarrow m=-\dfrac{1}{6}\)
b.
\(-2x-y=5\Leftrightarrow y=-2x-5\)
Để hai đường thẳng trùng nhau:
\(\Leftrightarrow\left\{{}\begin{matrix}2m=-2\\m-1=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m=-4\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
Vậy ko tồn tại m để 2 đường thẳng trùng nhau

PTHDGD: \(\left(2m-5\right)x-m-2=-3-x\)
2 đt cắt tại 1 điểm trên trục tung nên x=0
\(\Leftrightarrow-m-2=-3\Leftrightarrow m=1\)

Lời giải:
Giao điểm của 2 đường thẳng thuộc trục hoành nên có dạng $(a,0)$. Vì điểm này thuộc $(d_1):x+y=-1$ nên $a+0=-1\Rightarrow a=-1$
Vậy giao điểm của 2 ĐT trên là $(-1,0)$
Giao điểm này $\in (d_2)$ khi mà $m.(-1)+0=1$
$\Leftrightarrow m=-1$

Gọi \(A\left(x_0;y_0\right)\) là giao điểm \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}y_0=-3x_0-7\\y_0=2x_0+3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_0=-\dfrac{4}{5}\\y_0=-\dfrac{23}{5}\end{matrix}\right.\)
\(\Rightarrow M\left(-\dfrac{4}{5};-\dfrac{23}{5}\right)\)
Lời giải:
Phương trình hoành độ giao điểm:
\(12x+5-m=3x+3+m\)
\(\Leftrightarrow 9x=2m-2\Leftrightarrow x=\frac{2m-2}{9}\)
Khi đó: \(y=3x+3+m=3.\frac{2m-2}{9}+3+m=\frac{5m+7}{3}\)
Vậy giao điểm của \((d_1); (d_2)\) là \(\left(\frac{2m-2}{9}; \frac{5m+7}{3}\right)\)
a)
Giao điểm nằm trên trục tung nghĩa là hoành độ bằng $0$
\(\Leftrightarrow \frac{2m-2}{9}=0\Rightarrow m=1\)
b)
Giao điểm nằm bên trái trục tung nghĩa là hoành độ âm
\(\Leftrightarrow \frac{2m-2}{9}< 0\Leftrightarrow m< 1\)
c)
Giao điểm nằm ở góc phần tư thứ 2 nghĩa là hoành độ âm, tung độ dương
\(\Leftrightarrow \left\{\begin{matrix} \frac{2m-2}{9}< 0\\ \frac{5m+7}{3}>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m< 1\\ m> -1,4\end{matrix}\right.\)