Vẽ đồ thị hàm số \(y=f\left(x\right)=-3x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
3 tháng 2 2020
Giải
a) y = f(x) = 3x
Cho x = 1 thì y = 3 .1 = 3 ; A(1;3)
y x O A 1 3
b) y = f(x) = \(-\frac{1}{2}x\)
cho x = 2 thì y = 2 . \(-\frac{1}{2}\)= -1
y x O 2 -1
12 tháng 9 2023
a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
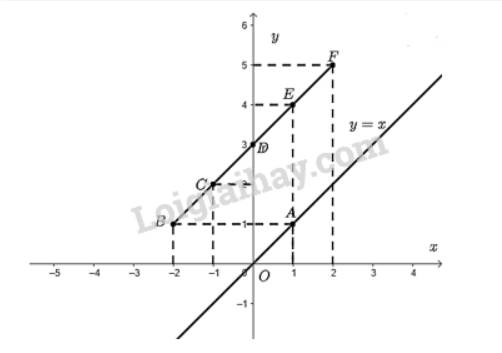
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
MH
4 tháng 4 2017
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =
= 3(-1) +2 = -1.
= (-1)2 – 1 = 0.
Vì 
nên không tồn tại 
. Vậy hàm số gián đoạn tại
x0 = -1.
BT
26 tháng 5 2017
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) D = (10.58, -5.6) D = (10.58, -5.6) D = (10.58, -5.6)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).
9 đko nhỉ
TM
5 tháng 9 2023
1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
a, Hệ số góc của cát tuyến PQ là \(k_{PQ}=\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}\)
b, Khi \(x\rightarrow x_0\) thì vị trí của điểm \(Q\left(x;f\left(x\right)\right)\) trên đồ thị (C) sẽ tiến gần đến điểm \(P\left(x_0;f\left(x_0\right)\right)\) và khi \(x=x_0\) thì hai điểm này sẽ trùng nhau.
c, Nếu điểm Q di chuyển trên (C) tới điểm P mà \(k_{PQ}\) có giới hạn hữu hạn k thì cát tuyến PQ cũng sẽ tiến đến gần vị trí tiếp tuyến của đồ thị (C) tại điểm P. Vì vậy, giới hạn của cát tuyến QP sẽ là đường thẳng tiếp tuyến tại điểm P
22 tháng 5 2022
b: Vì (Δ)//(d) nên m=-2
Vậy: (Δ): y=-2x+n
Phương trình hoành độ giao điểm là
\(-\dfrac{1}{2}x^2+x-n=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{-1}{2}\cdot\left(-n\right)=1-2n\)
Để (d) tiếp xúc với (P) thì -2n+1=0
hay n=1/2
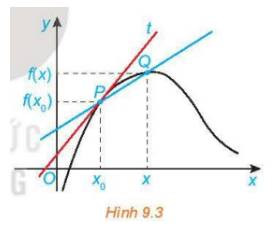
Bảng giá trị tương ứng của x và y
O 1 -3 -1 3 y=-3x
Vậy đths y = -3x là đường thẳng đi qua 2 điểm (1;-3) và (-1;3)
Cảm ơn cậu