Cho x, y ∈ R thỏa mãn x2 + y2 = 1. Tìm GTLN và GTNN của M = y2+\(\sqrt{3}xy\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
1
O
1
AH
Akai Haruma
Giáo viên
4 tháng 1 2021
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
VM
2
AH
Akai Haruma
Giáo viên
19 tháng 6 2021
Lời giải:
Áp dụng BĐT AM-GM:
$x^2+y^2\geq 2\sqrt{x^2y^2}=2|xy|\geq 2xy$
$\Rightarrow 3(x^2+y^2)\geq 6xy$
$x^2+9\geq 2\sqrt{9x^2}=2|3x|\geq 6x$
$y^2+9\geq 2\sqrt{9y^2}=2|3y|\geq 6y$
Cộng theo vế các BĐT trên:
$4(x^2+y^2)+18\geq 6(xy+x+y)=90$
$\Rightarrow x^2+y^2=18$
Vậy $A_{\min}=18$ khi $(x,y)=(3,3)$
AH
Akai Haruma
Giáo viên
20 tháng 6 2021
Sầu Riêng: của em nếu $x,y$ dương thì đúng. Còn trong bài $x,y$ thực thì đến đoạn $(x+y+2)^2\geq 64$ thì không khẳng định $x+y\geq 6$ được nha.
CM
15 tháng 3 2018
Ta có: 2 x 2 + 1 2 ≥ 2 x ; 2 y 2 + 1 2 ≥ 2 y và x 2 + y 2 ≥ 2 x y
Cộng vế với vế các BĐT trên ta được:
3 x 2 + y 2 + 1 ≥ 2 x + y + x y = 5 2
=> A = x 2 + y 2 ≥ 1 2
Từ đó tìm được A m i n = 1 2 <=> x = y = 1 2
TL
2
19 tháng 12 2018
\(M=\sqrt{3}xy+y^2=\frac{1}{2}\left(x^2+2\sqrt{3}xy+3y^2\right)-\frac{1}{2}x^2-\frac{1}{2}y^2\)
\(=\frac{1}{2}\left(x+\sqrt{3}y\right)^2-\frac{1}{2}\ge-\frac{1}{2}\).
Nên GTNN của M là \(-\frac{1}{2}\) đạt được khi \(x=-\sqrt{3}y\Rightarrow x^2=3y^2\Rightarrow4y^2=1\Rightarrow y=\pm\frac{1}{2}\)
+,Với \(y=\frac{1}{2}\Rightarrow x=-\frac{\sqrt{3}}{2}\)
+,Với \(y=-\frac{1}{2}\Rightarrow x=\frac{\sqrt{3}}{2}\)
Ta lại có:\(M=\sqrt{3}xy+y^2\le\frac{3x^2+y^2}{2}+y^2=\frac{3x^2+3y^2}{2}=\frac{3}{2}\)
Nên GTLN của M là \(\frac{3}{2}\) đạt được khi \(\sqrt{3}x=y\Rightarrow3x^2=y^2\Rightarrow4x^2=1\Rightarrow x=\pm\frac{1}{2}\)
+,Với \(x=\frac{1}{2}\Rightarrow y=\frac{\sqrt{3}}{2}\)
+,Với \(x=-\frac{1}{2}\Rightarrow y=-\frac{\sqrt{3}}{2}\)
19 tháng 12 2018
M=3xy+y2=21(x2+23xy+3y2)−21x2−21y2
=\frac{1}{2}\left(x+\sqrt{3}y\right)^2-\frac{1}{2}\ge-\frac{1}{2}=21(x+3y)2−21≥−21.
Nên GTNN của M là -\frac{1}{2}−21 đạt được khi x=-\sqrt{3}y\Rightarrow x^2=3y^2\Rightarrow4y^2=1\Rightarrow y=\pm\frac{1}{2}x=−3y⇒x2=3y2⇒4y2=1⇒y=±21
+,Với y=\frac{1}{2}\Rightarrow x=-\frac{\sqrt{3}}{2}y=21⇒x=−23
+,Với y=-\frac{1}{2}\Rightarrow x=\frac{\sqrt{3}}{2}y=−21⇒x=23
Ta lại có:M=\sqrt{3}xy+y^2\le\frac{3x^2+y^2}{2}+y^2=\frac{3x^2+3y^2}{2}=\frac{3}{2}M=3xy+y2≤23x2+y2+y2=23x2+3y2=23
Nên GTLN của M là \frac{3}{2}23 đạt được khi \sqrt{3}x=y\Rightarrow3x^2=y^2\Rightarrow4x^2=1\Rightarrow x=\pm\frac{1}{2}3x=y⇒3x2=y2⇒4x2=1⇒x=±21
+,Với x=\frac{1}{2}\Rightarrow y=\frac{\sqrt{3}}{2}x=21⇒y=23
+,Với x=-\frac{1}{2}\Rightarrow y=-\frac{\sqrt{3}}{2}x=−21⇒y=−23
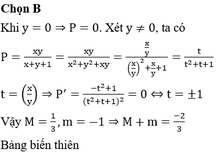
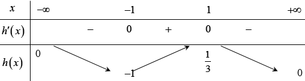
Đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(\Rightarrow M=cos^2a+\sqrt{3}.sina.cosa=\dfrac{cos2a+1}{2}+\dfrac{\sqrt{3}}{2}sin2a\)
\(\Rightarrow M=\dfrac{\sqrt{3}}{2}sin2a+\dfrac{1}{2}cos2a+\dfrac{1}{2}=sin2a.cos\left(\dfrac{\pi}{6}\right)+sin\left(\dfrac{\pi}{6}\right).cos2a+\dfrac{1}{2}=sin\left(2a+\dfrac{\pi}{6}\right)+\dfrac{1}{2}\)
Do \(-1\le sin\left(2a+\dfrac{\pi}{6}\right)\le1\Rightarrow\dfrac{-1}{2}\le M\le\dfrac{3}{2}\)
Vậy:
\(M_{min}=\dfrac{-1}{2}\) khi \(sin\left(2a+\dfrac{\pi}{6}\right)=-1\Rightarrow a=\dfrac{-\pi}{3}+k\pi\) \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{-\sqrt{3}}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\y=\dfrac{-1}{2}\end{matrix}\right.\end{matrix}\right.\)
\(M_{max}=\dfrac{3}{2}\) khi \(sin\left(2a+\dfrac{\pi}{6}\right)=1\) \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x=\dfrac{-1}{2}\\y=\dfrac{-\sqrt{3}}{2}\end{matrix}\right.\end{matrix}\right.\)