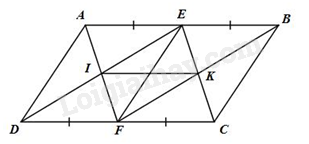
Cho hình bình hành ABCD. Gọi E. F lần lượt là trung điểm của AB và CD, G và H lần lượt là giao điểm của BD với AF và CE.
a, C/minh: Tứ giác AECF, GEHF là hình bình hành
b, C/minh: DG = GH = HB
c, Để tứ giác GEHF là hình chữ nhật thì hình bình hành ABCD cần thêm điều kiện gì ?
d, Để tứ giác GEHF là hình thoi thì hình bình hành ABCD cần thêm điều kiện gì ?