tìm x,y biết:
\(|x+5|+|2y-8|\)\(\le\)0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VH
13 tháng 10 2016
Vì số mũ của 2 số trên là 100 và 200, đều là số chẵn => Không số nào trong số trên là số âm => Tổng của chúng là số vô âm => Tổng của chúng = 0 => Các hiệu (3x-5) và tổng (2y+1) = 0
=> 3x - 5 = 0 => 3x = 5 => x = 5/3
=> 2y + 1 = 0 => 2y = -1 => y = -0,5
Vậy x = 5/3 và y = -0,5
<Spyofgame200 - NO COPPY>
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Vẽ các đường thẳng \(x + 2y = - 4\)(nét đứt) và \(y = x + 5\) (nét liền)
Thay tọa độ O vào \(x + 2y < - 4\) ta được: \(0 + 2.0 < - 4\) (Sai)
=> Gạch đi phần chứa O.
Thay tọa độ O vào \(y \ge x + 5\) ta được: \(0 \ge 0 + 5\) (Sai)
=> Gạch đi phần chứa O.
\(x + 2y = -4 => y = \frac{-4 - x}{2} \)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(x + 2y = - 4\) và \(y = x + 5\), ta được:
\( \frac{-4 - x}{2} = x + 5 \\ x = \frac{-14}{3} \\ => y = \frac{1}{3} \)
Miền nghiệm của hệ:
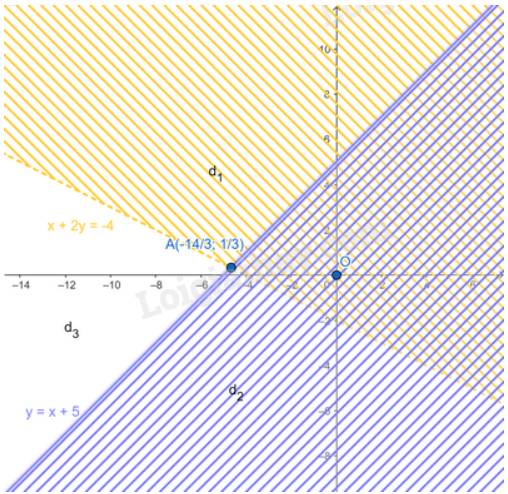
Từ hình vẽ ta thấy miền nghiệm của hệ là \(d_3\)
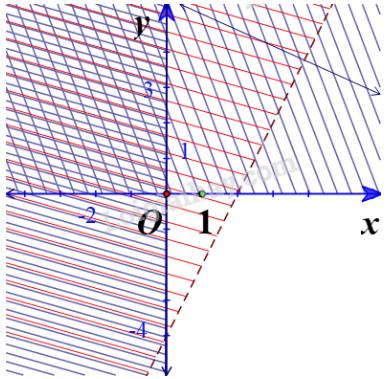
b) Vẽ các đường thẳng \(4x - 2y = 8\)(nét đứt) và hai trục (nét liền)
Thay tọa độ O vào \(4x - 2y > 8\) ta được: \(4.0 - 2.0 > 8\) (Sai)
=> Gạch đi phần chứa O.
Với \(x \ge 0\) thì gạch phần bên trái Oy
Với \(y \le 0\) thì gạch bên trên Ox
Miền nghiệm của hệ:
21 tháng 1 2017
\(\left|x+\frac{8}{5}\right|\ge0,\forall x\in R\)
\(\left|2.2-2y\right|\ge0,\forall y\in R\)
Do đó \(\left|x+\frac{8}{5}\right|+\left|2.2-2y\right|\ge0;\forall x,y\in R\)
Mà theo đề cho \(\left|x+\frac{8}{5}\right|+\left|2.2-2y\right|\le0\) suy ra \(\left|x+\frac{8}{5}\right|+\left|2.2-2y\right|=0\)
\(\Rightarrow\)\(\hept{\begin{cases}\left|x+\frac{8}{5}\right|=0\\\left|2.2-2y\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x+\frac{8}{5}=0\\2.2-2y=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{-8}{5}\\y=\frac{11}{10}\end{cases}}}\)
S
1
HP
23 tháng 12 2015
|x+8/5| > 0
|2,2-2y|>0
=>|x+8/5\+|2,2-2y|>0
mà |x+8/5|+|2,2-2y|<0
=>|x+8/5|=|2,2-2y|=0
=>x=-8/5 và 2y=2,2=>y=1,1
vậy x=-8/5=-1,6 và y=1,1
tick nhé
NK
1
2 tháng 2 2017
Vì |x - 3|2014 ≥ 0 ; |6 + 2y|2015 ≥ 0
=> |x - 3|2014 + |6 + 2y|2015 ≥ 0
Mà để |x - 3|2014 + |6 + 2y|2015 ≤ 0 <=> |x - 3|2014 = 0 ; |6 + 2y|2015 = 0
=> x = 3 và y = - 3
Vậy x = 3 và y = - 3
6 tháng 9 2021
a) x2+y2-4x+4y+8=0
⇔ (x-2)2+(y+2)2=0
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)
b)5x2-4xy+y2=0
⇔ x2+(2x-y)2=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
c)x2+2y2+z2-2xy-2y-4z+5=0
⇔ (x-y)2+(y-1)2+(z-2)2=0
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\y-1=0\\z-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\z=2\end{matrix}\right.\)
6 tháng 9 2021
b: Ta có: \(5x^2-4xy+y^2=0\)
\(\Leftrightarrow x^2-\dfrac{4}{5}xy+y^2=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot\dfrac{2}{5}y+\dfrac{4}{25}y^2+\dfrac{21}{25}y^2=0\)
\(\Leftrightarrow\left(x-\dfrac{2}{5}y\right)^2+\dfrac{21}{25}y^2=0\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
MH
3
17 tháng 6 2019
Tham khảo bài 8 trong link: Câu hỏi của Nguyễn Linh Chi - Toán lớp - Học toán với OnlineMath
26 tháng 3 2020
Tham khảo link này : https://olm.vn/hoi-dap/detail/223163065606.html