\(|5x+10|\)+\(|6y-9|\le0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2016
Vì: \(\begin{cases}\left|5x+1\right|\ge0\\\left|6y-8\right|\ge0\end{cases}\)\(\Rightarrow\left|5x+1\right|+\left|6y-8\right|\ge0\)
Mà \(\left|5x+1\right|+\left|6y-8\right|\le0\)
=> \(\begin{cases}5x+1=0\\6y-8=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=-\frac{1}{5}\\y=\frac{4}{3}\end{cases}\)
25 tháng 10 2016
|5x+1|+|6x-8|\(\le\)0
Trường hợp 1:
|5x+1|+|6x-8|=0
\(\Rightarrow\)5x+1=0
x =0-1
x =-1
x =\(\frac{-1}{5}\)
\(\Rightarrow\)6y-8=0
6y =8
y =\(\frac{4}{3}\)
Trường hợp 2:|5x+1|+|6y-8|<0
sẽ k có giá trị của x hay y nào thoả mãn vì giá trị tuyệt đối lun dương
H
1
30 tháng 7 2021
1)\(\sqrt{4x^2+12x+9}=2-x\)
\(\Leftrightarrow\sqrt{\left(2x+3\right)^2}=2-x\)
\(\Leftrightarrow\left|2x+3\right|=2-x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=2-x\\2x+3=x-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-1\\x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-5\end{matrix}\right.\)
\(\)
22 tháng 12 2017
a)Với mọi \(x;y\in R\) ta có: \(2017\left|2x-y\right|^{2008}+2008\left|y-4\right|^{2007}\ge0\)
mà \(2007\left|2x-y\right|^{2008}+2008\left|y-4\right|^{2007}\le0\)
\(\Rightarrow2007\left|2x-y\right|^{2008}+2008\left|y-4\right|^{2007}=0\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\)
b) Với mọi \(x;y\in R\) ta có: \(\left|5x+1\right|+\left|6y-8\right|\ge0\)
mà \(\left|5x+1\right|+\left|6y-8\right|\le0\)
\(\Rightarrow\left|5x+1\right|+\left|6y-8\right|=0\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=\dfrac{4}{3}\end{matrix}\right.\)
CG
1
22 tháng 2 2020
Đkxđ: \(x\ne2;x\ne3\)
Ta có \(x^2-3x+9=\left(x-\frac{3}{2}\right)^2+\frac{27}{4}\ge\frac{27}{4}>0\)
\(\Rightarrow\frac{x^2-3x+9}{x^2-5x+6}< 0\)khi và chỉ khi \(x^2-5x+6< 0\Leftrightarrow\left(x-2\right)\left(x-3\right)< 0\)
Vì \(x-2>x-3\Rightarrow\hept{\begin{cases}x-2>0\\x-3< 0\end{cases}\Rightarrow2< x< 3}\)
Vậy \(2< x< 3\)
DK
0
UN
1
GL
24 tháng 9 2023
\(f,\dfrac{x^2-6x+9}{x^2-8x+15}\\ =\dfrac{\left(x-3\right)^2}{\left(x-3\right)\left(x-5\right)}\\ =\dfrac{x-3}{x-5}\\ l,\dfrac{5xy+5x+3+3y}{10xy-15x-9+6y}\\ =\dfrac{5x\left(y+1\right)+3\left(y+1\right)}{5x\left(2y-3\right)+3\left(2y-3\right)}\\ =\dfrac{\left(y+1\right)\left(5x+3\right)}{\left(2y-3\right)\left(5y+3\right)}\\ =\dfrac{y+1}{2y-3}\)
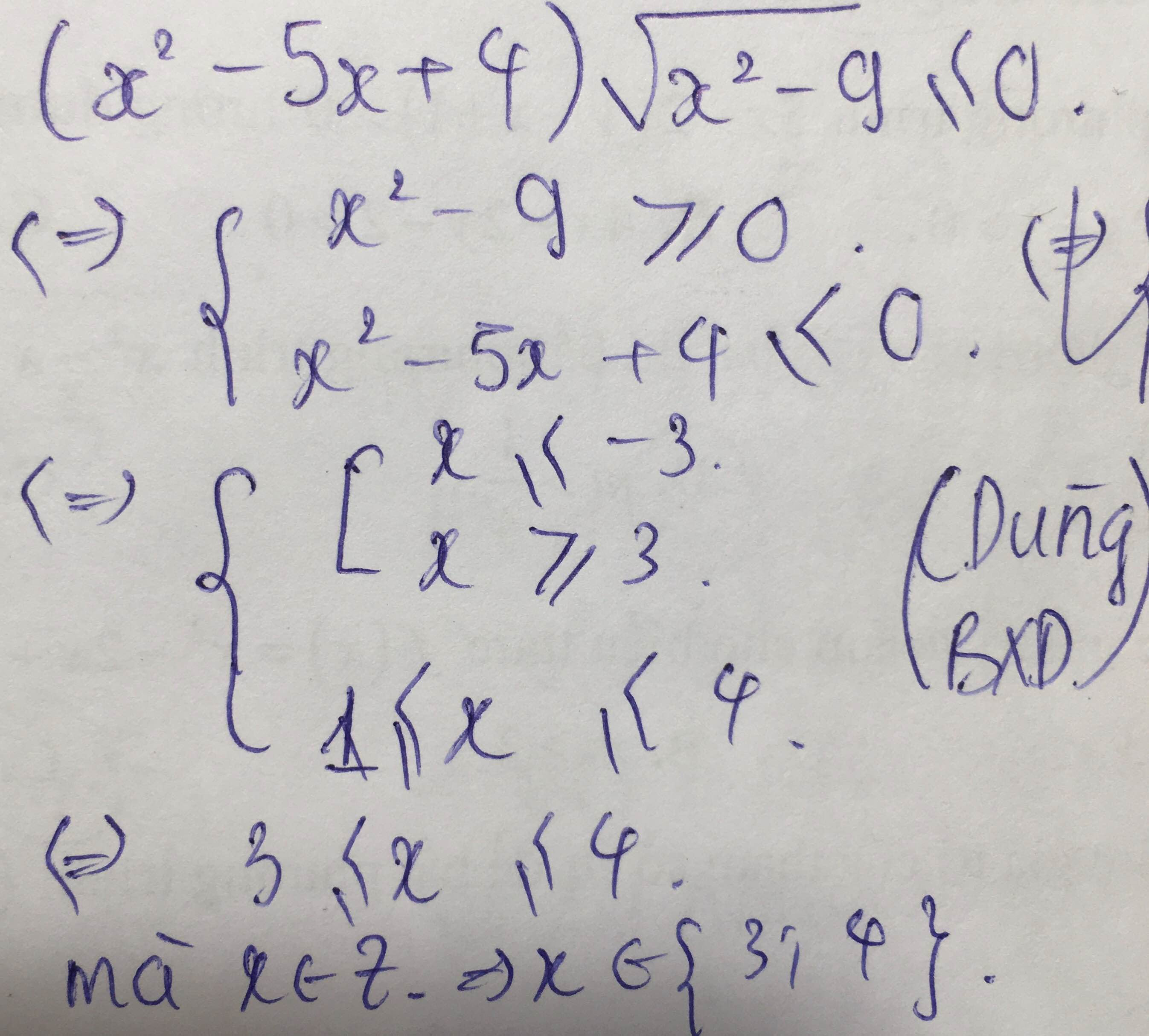
\(Taco\)
\(|5x+10|,|6y-9|\ge0\)
\(Mà:|5x+10|,|6y-9|=0\Rightarrow|5x+10|=|6y-9|=0\)
\(\Rightarrow x=-2;y=1,5\)
\(\left|5x+10\right|+\left|6y-9\right|\le0\)
\(\Rightarrow\hept{\begin{cases}\left|5x+10\right|=0\\\left|6y-9\right|=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}5x=-10\\6y=9\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=-2\\y=\frac{3}{2}\end{cases}}\)