4x-12-x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 11 2023
a: \(x^3-4x^2-x+4=0\)
=>\(\left(x^3-4x^2\right)-\left(x-4\right)=0\)
=>\(x^2\left(x-4\right)-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(x^2-1\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x^2=1\end{matrix}\right.\Leftrightarrow x\in\left\{2;1;-1\right\}\)
b: Sửa đề: \(x^3+3x^2+3x+1=0\)
=>\(x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=0\)
=>\(\left(x+1\right)^3=0\)
=>x+1=0
=>x=-1
c: \(x^3+3x^2-4x-12=0\)
=>\(\left(x^3+3x^2\right)-\left(4x+12\right)=0\)
=>\(x^2\cdot\left(x+3\right)-4\left(x+3\right)=0\)
=>\(\left(x+3\right)\left(x^2-4\right)=0\)
=>\(\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\\x=-2\end{matrix}\right.\)
d: \(\left(x-2\right)^2-4x+8=0\)
=>\(\left(x-2\right)^2-\left(4x-8\right)=0\)
=>\(\left(x-2\right)^2-4\left(x-2\right)=0\)
=>\(\left(x-2\right)\left(x-2-4\right)=0\)
=>(x-2)(x-6)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)
SX
0
NT
5
11 tháng 9 2017
a) \(x^3\)\(-\)\(\frac{1}{4}x\)\(=\)\(0\)
\(x\left(x^2-\frac{1}{4}\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x^2-\frac{1}{4}=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x^2=0,5^2\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x=+-0,5\end{cases}}\)
Vậy .............................
b) \(\left(2x-1\right)^2\)\(-\)\(\left(x+3\right)^2\)\(=\)\(0\)
\(\left(2x-1+x+3\right)\left(2x-1-x-3\right)=0\)
\(\left(3x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}3x+2=0\\x-4=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}3x=-2\\x=4\end{cases}}\)\(\orbr{\begin{cases}x=\frac{-2}{3}\\x=4\end{cases}}\)
Vậy ................................
c) \(x^2\)\(\left(x-3\right)\)\(+\)\(12\)\(-\)\(4x\)\(=\)\(0\)
\(x^2\)\(\left(x-3\right)\)\(-\)\(4\)\(\left(x-3\right)\)\(=\)\(0\)
\(\left(x^2-4\right)\left(x-3\right)\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x^2\\x-3=0\end{cases}-4=0}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x^2\\x=3\end{cases}=2^2}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=+-2\\x=3\end{cases}}\)
11 tháng 9 2017
a)\(x^3-\frac{1}{4}x=0\)
\(\Leftrightarrow x\left(x^2-\frac{1}{4}\right)=0\)
\(\Leftrightarrow x\left(x-\frac{1}{2}\right)\left(x+\frac{1}{2}\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\x-\frac{1}{2}=0\\x+\frac{1}{2}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}}\)
HD
1
6 tháng 10 2018
\(x^3-3x^2-4x+12=0\)
\(\Rightarrow x^2\left(x-3\right)-4\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x^2-4\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x-2\right)\left(x+2\right)=0\)
Tìm được x = 3, x = 2 và x = -2
\(x^4+x^3-4x-4=0\)
\(\Rightarrow x^3\left(x+1\right)-4\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x^3-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+1=0\\x^3=4\end{cases}\Rightarrow\orbr{\begin{cases}x=-1\\x=\sqrt[3]{4}\end{cases}}}\)
Chúc bạn học tốt.
KN
13 tháng 7 2019
\(x^2+4x-12=0\)
\(\Leftrightarrow x^2+4x+4=16\)
\(\Leftrightarrow\left(x+2\right)^2=16\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=\sqrt{16}\\x+2=-\sqrt{16}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x+2=4\\x+2=-4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-6\end{cases}}\)
Vậy tập nghiệm của pt là \(S=\left\{-6;2\right\}\)
TA
1
13 tháng 10 2021
c: Ta có: \(x^3+3x^2+3x-7=0\)
\(\Leftrightarrow x+1=2\)
hay x=1
b: Ta có: \(x\left(x-3\right)-4x+12=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
27 tháng 3 2020
a) Ta có: \(x^2-9x+20=0\)
\(\Leftrightarrow x^2-5x-4x+20=0\)
\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\end{matrix}\right.\)
Vậy: x∈{4;5}
b) Ta có: \(x^3-4x^2+5x=0\)
\(\Leftrightarrow x\left(x^2-4x+5\right)=0\)(1)
Ta có: \(x^2-4x+5\)
\(=x^2-4x+4+1=\left(x-2\right)^2+1\)
Ta có: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2+1\ge1>0\forall x\)
hay \(x^2-4x+5>0\forall x\)(2)
Từ (1) và (2) suy ra x=0
Vậy: x=0
c) Sửa đề: \(x^2-2x-15=0\)
Ta có: \(x^2-2x-15=0\)
\(\Leftrightarrow x^2+3x-5x-15=0\)
\(\Leftrightarrow x\left(x+3\right)-5\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)
Vậy: x∈{-3;5}
d) Ta có: \(\left(x^2-1\right)^2=4x+1\)
\(\Leftrightarrow x^4-2x^2+1-4x-1=0\)
\(\Leftrightarrow x^4-2x^2-4x=0\)
\(\Leftrightarrow x\left(x^3-2x-4\right)=0\)
\(\Leftrightarrow x\left(x^3+2x^2+2x-2x^2-4x-4\right)=0\)
\(\Leftrightarrow x\cdot\left[x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\right]=0\)
\(\Leftrightarrow x\cdot\left(x^2+2x+2\right)\cdot\left(x-2\right)=0\)(3)
Ta có: \(x^2+2x+2\)
\(=x^2+2x+1+1=\left(x+1\right)^2+1\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+1\right)^2+1\ge1>0\forall x\)
hay \(x^2+2x+2>0\forall x\)(4)
Từ (3) và (4) suy ra
\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy: x∈{0;2}
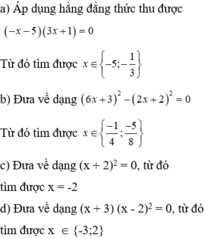
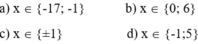
3x - 12 = 0
x = 4
\(\Rightarrow3x=12\Rightarrow x=4\)