Cho tam giác ABC vuông tại A. Gọi M là trung điên của BC. Trên tia AM lấy điểm D sao cho MD=MA.
a) chứng minh tam giác ABM= t giác ECM
b) chứng minh: AC vuông góc với CD
Ai giúp mk với đang ôn thi <3 <3 <3
Giúp câu b thôi nha mà phải làm câu a trước
Mk làm câu a rồi câu b mk k biết ai biết cứu giúp nhaaa !!!

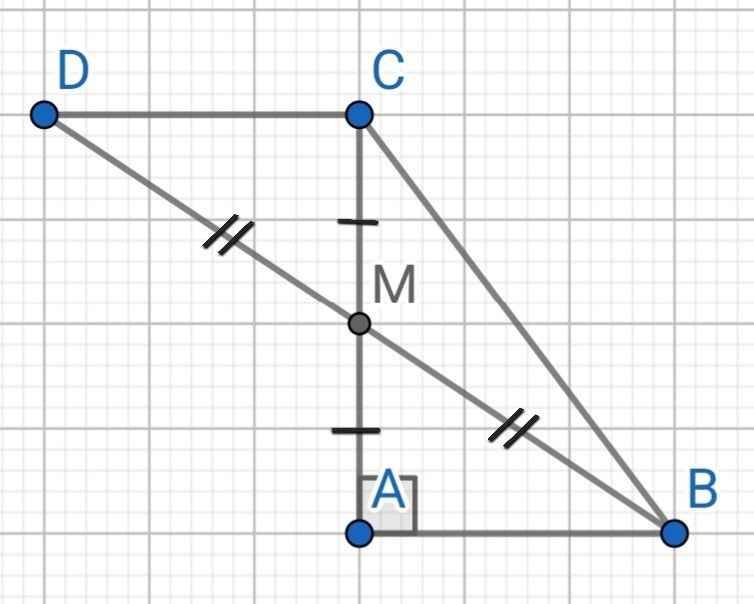
Câu a sao lại là t giác ECM hả bn
DCM mk lộn sorry bạn giúp mk đi