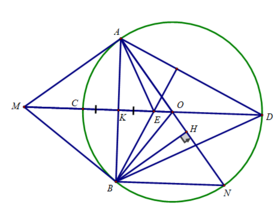
- Cho (O, R) một đường thẳng d cắt đường tròn (O) tại C và D, lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M, qua M vẽ tiếp tuyến MA, MB với đường tròn. Gọi H là trung điểm cyar CD, OM cắt AB tại E, Chứng minh rằng:
a> AB vuông góc với OM
b> Tích OE, OM không đổi
c> Khi M di chuyển trên đường thẳng d thì đường thẳng AB đi qua 1 điểm cố định.

a: Xét (O) có
MA,MB là các tiếp tuyên
nên MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM vuông góc với AB
b: Xét ΔOBM vuông tại B có BElà đường cao
nên OE*OM=OB^2=R^2 ko đổi