\sqrt{x}>2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2017
GIAO LUU
\(Lim_{x\rightarrow vc}=\frac{x+\sqrt{x+\sqrt{x}}-x}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}=\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}\\ \)
\(\Leftrightarrow Lim_{x\rightarrow vc}=\frac{\sqrt{\frac{x+\sqrt{x}}{x}}}{\sqrt{\frac{x+\sqrt{x+\sqrt{x}}}{x}}+1}=\frac{\sqrt{1+\frac{1}{\sqrt{x}}}}{\sqrt{1+\sqrt{\frac{x+\sqrt{x}}{x^2}}}+1}\\ \)
\(\Leftrightarrow\frac{Lim}{x\rightarrow+vc}=\frac{\sqrt{1+\frac{1}{\sqrt{x}}}}{\sqrt{1+\sqrt{\frac{1}{x}+\frac{1}{\sqrt{x^3}}}}+1}=\frac{\sqrt{1+\frac{1}{+vc}}}{\sqrt{1+\sqrt{\frac{1}{+vc}+\frac{1}{+vc}}}+1}=\frac{\sqrt{1+0}}{\sqrt{1+\sqrt{0+0}}+1}=\frac{1}{2}\)
21 tháng 5 2022
a: \(=\dfrac{x+2\sqrt{xy}+y-x+2\sqrt{xy}-y}{x-y}\cdot\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{4xy}{\left(x-y\right)\left(\sqrt{x}+\sqrt{y}\right)}\)
b: \(=\sqrt{x}+\sqrt{y}-\left(\sqrt{x}-\sqrt{y}\right)-2\sqrt{y}\)
\(=\sqrt{x}-\sqrt{y}-\sqrt{x}+\sqrt{y}=0\)
c: \(=\dfrac{x-1-4\sqrt{x}+\sqrt{x}+1}{x-1}\cdot\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-3\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}-2}\)
NQ
Nguyễn Quốc Đạt
CTVVIP
10 tháng 9 2023
\(x+\sqrt{x}=\sqrt{x}\left(\sqrt{x}+1\right)\\ x-\sqrt{x}=\sqrt{x}\left(\sqrt{x}-1\right)\\ a+3\sqrt{a}-10=a+5\sqrt{a}-2\sqrt{a}-10=\sqrt{a}\left(\sqrt{a}+5\right)-2\left(\sqrt{a}+5\right)=\left(\sqrt{a}-2\right)\left(\sqrt{a}+5\right)\)
\(x\sqrt{x}+\sqrt{x}-x-1=\left(x\sqrt{x}-x\right)+\left(\sqrt{x}-1\right)=x\left(\sqrt{x}-1\right)+\sqrt{x}-1=\left(\sqrt{x}-1\right)\left(x+1\right)\\ x+\sqrt{x}-2=x+2\sqrt{x}-\sqrt{x}-2=\sqrt{x}\left(\sqrt{x}+2\right)-\left(\sqrt{x}+2\right)=\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)\\ x-5\sqrt{x}+6=x-2\sqrt{x}-3\sqrt{x}-6=\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)=\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)\)
Mấy bạn còn lại tương tự những bài trên nhé. Nếu còn thắc mắc ở chỗ nào bạn có thể liên hệ mình nhé. Nhớ lần sau bạn tách ra nha, chứ nhiều câu quá.
AH
Akai Haruma
Giáo viên
10 tháng 9 2023
Khi phân tích thành nhân tử thì việc để dạng phân số kiểu 1/x là không đúng bạn nhé.
H9
HT.Phong (9A5)
CTVHS
16 tháng 8 2023
\(\left(\dfrac{1}{\sqrt{x}}-\sqrt{x}\right):\left(\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\) (ĐK: \(x>0\))
\(=\left(\dfrac{1}{\sqrt{x}}-\dfrac{x}{\sqrt{x}}\right)\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{-\sqrt{x}}\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{-\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\left(\sqrt{x}+1\right)^2\)
17 tháng 8 2023
c: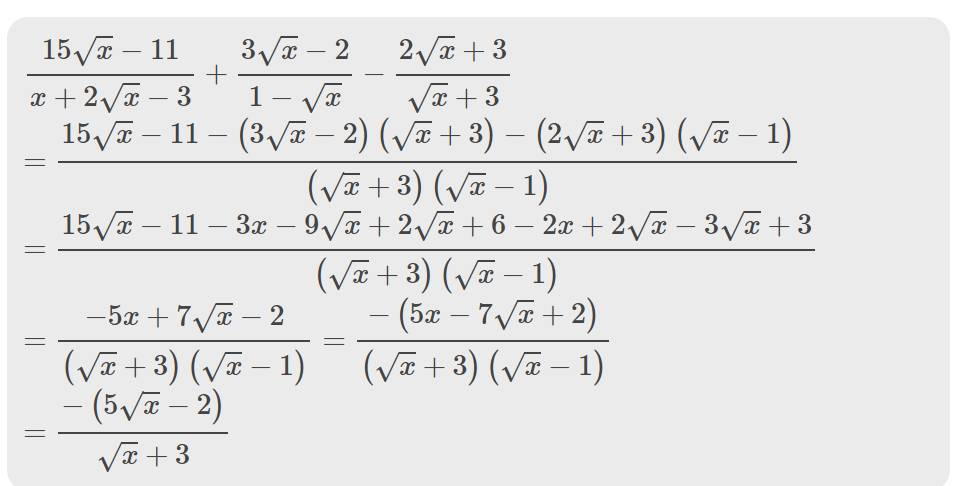 
b;
Sửa đề: \(\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2\sqrt{x}\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2x-6\sqrt{x}+x-4\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}-x+16\sqrt{x}-16}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{x+16}{\sqrt{x}+3}\)
26 tháng 8 2021
\(A=\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}=x-\sqrt{xy}+y\)
\(B=\dfrac{\sqrt{x}-\sqrt{y}}{x\sqrt{x}-y\sqrt{y}}=\dfrac{1}{x+\sqrt{xy}+y}\)
\(C=\dfrac{3\sqrt{3}+x\sqrt{x}}{3-\sqrt{3x}+x}=\sqrt{x}+\sqrt{3}\)
\(D=\dfrac{x+\sqrt{5x}+5}{x\sqrt{x}-5\sqrt{5}}=\dfrac{1}{\sqrt{x}-\sqrt{5}}\)