Thay số các chữ số thích hợp cho các chữ trong phép nhân sau :
abcdmn.2=cdmnab
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì 3a12b chia hết cho15 nên 3a12b sẽ chia hết cho 3 và 5
Để 3a12b chia hết cho 5 thì 3a12b phải tận cùng là 0 hoặc 5
Nếu 3a12b tận cùng là 0 thì 3a12b= 3a120
Để 3a120 chia hết cho 3 thì (3+a+1+2+0) \(⋮\)3
=> (6+a)\(⋮\)3
=> a= 0 hoặc a=3 hoặc a= 6
Nếu 3a12b tận cùng là 5 thì 3a12b= 3a125
Sau bn tự trình bày nhaa


ta có:
ab.cc=abcabc:abc
ab.cc=1001
ab.c.11=1001
ab.c=91
Vì 91=91.1=13.7
Nếu ab=91, c=1 (loại vì b=c=1)
Vậy ab=13, c=7. Ta Được
13.77.137=137137

Ta có : abab = 101 x ab
101 x ab + ab = 1326
102 x ab = 1326
ab = 13

a) Ta viết lại thành phép nhân:
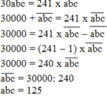
b) Ta có: abab = 101 x ab
101 x ab + ab = 1326
102 x ab = 1326
ab = 13
Đặt \(\overline{ab}=x,\overline{cd}=y,\overline{mn}=z\). Theo bài ra ta có:
\(2\left(10000x+100y+z\right)=10000y+100z+x\)
\(\Leftrightarrow20000x+200y+2z=10000y+100z+x\)
\(\Leftrightarrow19999x=9800y+98z\)
\(\Leftrightarrow19999x=98\left(100y+z\right)\)
\(\Leftrightarrow2857\overline{x}=14\left(100y+z\right)\)
\(\Leftrightarrow2857\overline{ab}=14\overline{cdmn}\)
Do đó \(2857\overline{ab}⋮14\). Mà (2857, 14) = 1 nên \(\overline{ab}⋮14\Leftrightarrow\overline{ab}\in\left\{14;28;42;56;70;84;98\right\}\)
Vì \(14\overline{cdmn}\le14.9999=139986\) nên \(\overline{ab}\le47\). Do đó \(\overline{ab}\in\left\{14;28;42\right\}\).
Đến đây thử từng TH