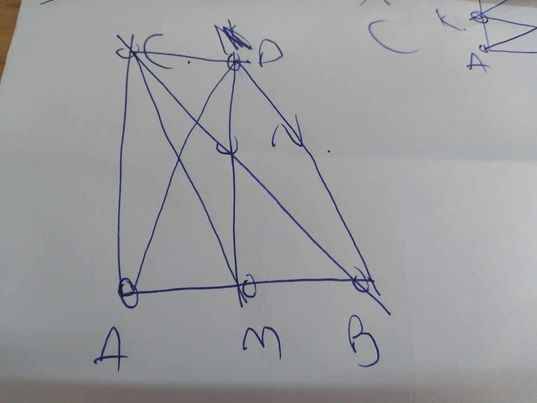
Cho tam giác ABC vuông tại A có AB= a. Gọi M, N, D lần lượt là trung điểm của AB, BC,AC.
a) Chứng minh ND là đường trung bình của tam giác ABC và tính độ dài của ND theo a.
b) Chứng minh tứ giác ADNM là hình chữ nhật.
c) Gọi Q là điểm đối xứng của N qua M. Chứng minh AQBN là hình thoi.
d) Trên tia đối của tia DB lấy điểm K sao cho DK= DB. Chứng minh 3 điểm Q, A, K thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 10 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
b: Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
17 tháng 12 2023
a: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: MN//BC
D\(\in\)NM
Do đó; MD//CB
ta có: \(MN=\dfrac{CB}{2}\)
\(MN=\dfrac{MD}{2}\)
Do đó:CB=MD
Xét tứ giác BMDC có
BC//MD
BC=MD
Do đó: BMDC là hình bình hành
b: Xét tứ giác AMCD có
N là trung điểm chung của AC và MD
nên AMCD là hình bình hành
TM
11 tháng 9 2021
a/ M, N là trung điểm của AB, AC ⇒ MN là đường trung bình của △ABC, MN // BC (1)
Vậy: MNCB là hình thang (đpcm)
==========
b/ Do MN là đường trung bình của △ABC
Vậy: \(MN=\dfrac{BC}{2}\Rightarrow BC=MN.2=3,5.2=7cm\)
==========
c/ Do E là trung điểm của BC \(\Rightarrow CE=\dfrac{BC}{2}\)
- Mà \(MN=\dfrac{BC}{2}\Rightarrow MN=CE\left(2\right)\)
Từ (1) và (2). Vậy: MNCE là hình bình hành (đpcm)
3 tháng 10 2021
a) Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> MN//AC
Mà AC⊥AB(tam giác ABC vuông tại A)
=> MN⊥AB(từ vuông góc đến song song)
b) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(pytago\right)\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-12^2=25\Rightarrow AC=5\left(cm\right)\)
Ta có: MN là đường trung bình tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.5=2,5\left(cm\right)\)
14 tháng 12 2022
a: Xét ΔCAB có CE/CA=CD/CB
nên ED//AB và ED=AB/2
=>AEDB là hình thang
mà góc EAB=90 độ
nênAEDB là hình thang vuông
b: Xét tứ giác ABKC có
D là trung điểm chung của AK và BC
góc BAC=90 độ
Do đó: ABKC là hình chữ nhật
3 tháng 1
a: Xét tứ giác BMCD có
N là trung điểm chung của BC và MD
=>BMCD là hình bình hành
b: Ta có: BMCD là hình bình hành
=>BM//CD và BM=CD
Ta có: BM//CD
M\(\in\)AB
Do đó: AM//CD
ta có: BM=CD
AM=MB
Do đó: AM=CD
Xét tứ giác AMDC có
AM//DC
AM=DC
Do đó: AMDC là hình bình hành
Hình bình hành AMDC có \(\widehat{MAC}=90^0\)
nên AMDC là hình chữ nhật
c: Ta có: AMDC là hình chữ nhật
=>\(\widehat{DMA}=90^0\)
=>DM\(\perp\)AB tại M
Xét ΔDBA có
DM là đường cao
DM là đường trung tuyến
Do đó: ΔDBA cân tại D
