tìm x biết :7^x-7^x+2=-2352
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CB
1
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(7^{x+2}+7^x\cdot2=51\\ \Leftrightarrow7^x\cdot7^2+7^x\cdot2=51\\ \Leftrightarrow7^x\cdot51=51\\ \Leftrightarrow7^x=1\\ \Leftrightarrow x=0\)
31 tháng 10 2021
\(\Rightarrow x-1=\dfrac{6}{7}+\dfrac{1}{7}\times\left(\dfrac{2}{7}+\dfrac{5}{7}\right)=\dfrac{6}{7}+\dfrac{1}{7}\times1\\ \Rightarrow x-1=\dfrac{6}{7}+\dfrac{1}{7}=1\\ \Rightarrow x=1+1=2\)
AH
Akai Haruma
Giáo viên
17 tháng 8
Lời giải:
$49x=|2x+7|+|2x+7^2|+....+|2x+7^{50}|\geq 0$
$\Rightarrow x\geq 0$
$\Rightarrow 2x+7>0; 2x+7^2>0;....; 2x+7^{50}>0$
Do đó bài toán trở thành:
$(2x+7)+(2x+7^2)+....+(2x+7^{50})=49x$
$\underbrace{(2x+2x+...+2x)}_{50}+(7+7^2+....+7^{50})=49x$
$\Rightarrow 100x+(7+7^2+....+7^{50})=49x$
$\Rightarrow 7+7^2+....+7^{50} = -51x>0$
$\Rightarrow x<0$ (vô lý - loại)
Vậy không tồn tại $x$ thỏa mãn đề.
7 tháng 10 2021
Bài 1:
a) \(=\dfrac{8}{15}\left(\dfrac{7}{13}+\dfrac{6}{13}\right)=\dfrac{8}{15}.1=\dfrac{8}{15}\)
b) \(=\dfrac{3.3-7-2.4}{12}=-\dfrac{6}{12}=-\dfrac{1}{2}\)
Bài 2:
\(\dfrac{x}{2,7}=-\dfrac{2}{3,6}\Rightarrow x=\dfrac{\left(-2\right).2,7}{3,6}\Rightarrow x=-\dfrac{3}{2}\)
Bài 3:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=-\dfrac{21}{7}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).2=-6\\y=\left(-3\right).5=-10\end{matrix}\right.\)
18 tháng 2 2020
Các bạn giúp mình giải với nhé! Đúng thì mình k đúng nhé. Cảm ơn các bạn nhiều lắm. Yêu cả nhà.
28 tháng 2 2021
\(1.\left(x-5\right)^{23}.\left(y+2\right)^7=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0\\\left(y+2\right)^7=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0^{23}\\\left(y+2\right)^7=0^7\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x-5=0\\y+2=0\end{cases}\Rightarrow\hept{\begin{cases}x=0+5\\y=0-2\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}\)
Vậy \(\left(x;y\right)=\left(5;-2\right)\)
NT
5
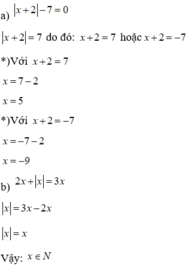
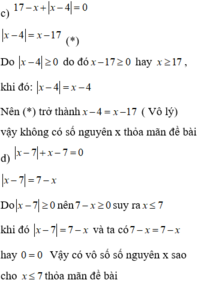
\(7^x-7^{x+2}=-2352=7^x-7^x.7^2\Rightarrow7^x-7^x.49=-2352\Rightarrow7^x.-48=-2352\)
\(\Rightarrow7^x=-2352:-48=49=7^2\Rightarrow x=2\)
\(7^x-7^{x+2}=-2352\)
\(7^x\left(1-49\right)=-2352\)
\(7^x.\left(-48\right)=-2352\)
\(\Rightarrow7^x=49\Leftrightarrow x=2\)