cho A(2,1) và B(-3,2). vết phương trình đường trung trực của đường thẳng AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KC
1
AH
Akai Haruma
Giáo viên
28 tháng 1
Lời giải:
$\overrightarrow{AB}=(2,-6)$
PT đường trung trực của $AB$ gọi là $(d)$.
$(d)\perp AB\Rightarrow VTPT(d) = \overrightarrow{AB}=(2,-6)$
$\Rightarrow VTCP(d) = (6,2)$ (1)
$(d)$ đi qua trung điểm của $AB$ là $(2,-1)$ (2)
Từ (1); (2)$ suy ra PTTS của $(d)$ là: \(\left\{\begin{matrix} x=2+6t\\ y=-1+2t\end{matrix}\right.\)
CM
11 tháng 8 2017
Gọi M trung điểm của AB nên M( 2; 1)
Ta có 
Gọi d là đường thẳng trung trực của AB
thì d qua M(2; 1) và nhận 
làm VTPT.
Phương trình đường thẳng d là:
1( x- 2) – 6.(y -1) =0
Hay x- 6y+ 4= 0.
Chọn D
CM
30 tháng 3 2017
Gọi M( 1; 3) là trung điểm của AB.
Ta có 
Gọi d là đường thẳng trung trực của AB thì d qua M( 1;3) và nhận 
làm VTCP nên có phương trình tham số là:
Chọn A.
LT
1
14 tháng 4 2023
vecto AB=(-4;4)=(-1;1)
Tọa độ trung điểm của AB là:
x=(-1-5)/2=-6/2=-3 và y=(-1+3)/2=1
Phương trình trung trực của AB là:
-1(x+3)+1(y-1)=0
=>-x-3+y-1=0
=>-x+y-4=0
CM
17 tháng 11 2017
Đáp án: B
Gọi I là trung điểm của AB ⇒ I(0;-1)
A(1;-3), B(-1;1)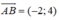 
Đường thẳng trung trực của AB là đường thẳng đi qua I và nhận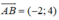 
là vecto pháp tuyến: -2(x - 0) + 4(y + 1) = 0 ⇔ x - 2y - 2 = 0
HN
21 tháng 3 2022
Gọi M(2;1) và d lần lượt là trung điểm và đường trung trực của AB.
Một vectơ pháp tuyến của d là \(\overrightarrow{n}\)=\(\overrightarrow{AB}\)=(2;0).
Phương trình cần tìm:
d: 2.(x-2)+0.(y-1)=0 \(\Rightarrow\) x=2.
CM
2 tháng 7 2017
ĐÁP ÁN B
Gọi M là trung điểm của AB. Tọa độ M là: x = 3 + ( − 1 ) 2 = 1 y = 4 + 2 2 = 3 ⇒ M ( 1 ; 3 )
Đường thẳng trung trực của đoạn AB đi qua trung điểm M(1;3) của đoạn AB và có vectơ pháp truyến n → = A B → = − 4 ; − 2 = − 2 2 ; 1 nên phương trình trung trực là:
2(x – 1) + (y – 3) = 0 ⟺ 2x + y – 5 = 0
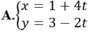
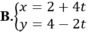
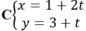
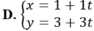
\(\overrightarrow{AB}=\left(-5;1\right)\)
Tọa độ I là trung điểm của AB là:
\(\left\{{}\begin{matrix}x=\dfrac{2-3}{2}=\dfrac{-1}{2}\\y=\dfrac{1+2}{3}=\dfrac{3}{2}\end{matrix}\right.\)
Phương trình đường trung trực của AB là:
-5(x+1/2)+1(y-3/2)=0
=>-5x-5/2+y-3/2=0
=>-5x+y-1=0