ptđttnt: 2x3-12x2+18x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
4
2 tháng 11 2021
\(2x^3-12x^2+18x=2x\left(x^2-6x+9\right)=2x\left(x-3\right)^2\)
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Câu 1:
a) 2x(3x+2) - 3x(2x+3) = 6x^2+4x - 6x^2-9x = -5x
b) \(\left(x+2\right)^3+\left(x-3\right)^2-x^2\left(x+5\right)\)
\(=x^3+6x^2+12x+8+x^2-6x+9-x^3-5x^2\)
\(=2x^2+6x+17\)
c) \(\left(3x^3-4x^2+6x\right)\div\left(3x\right)=x^2-\dfrac{4}{3}x+2\)
TT
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
1 tháng 8 2023
\(2x-x^2=2\\ \Leftrightarrow x^2-2x+2=0\\ \Leftrightarrow\left(x^2-2x+1\right)+1=0\\ \Leftrightarrow\left(x-1\right)^2+1=0\\ Mà:\left(x-1\right)^2\ge0\forall x\in R\\ \Rightarrow\left(x-1\right)^2+1\ge1\forall x\in R\\ Vậy:Pt.vô.nghiệm\\ x^3+15x^2+75x+125=0\\ x^3+3.x^2.5+3.x.5^2+5^3=0\\ \left(x+5\right)^3=0\\ \Leftrightarrow x+5=0\\ \Leftrightarrow x=-5\\ x^3+48x=12x^2+64\\ \Leftrightarrow x^3-12x^2+48x-64=0\\ \Leftrightarrow x^3-3.x^2.4+3.x.4^2-4^2=0\\ \Leftrightarrow\left(x-4\right)^3=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)
23 tháng 4 2023
a: x^3-2x-4=0
=>x^3-2x^2+2x^2-4x+2x-4=0
=>(x-2)(x^2+2x+2)=0
=>x-2=0
=>x=2
b: 2x^3-12x^2+17x-2=0
=>2x^3-4x^2-8x^2+16x+x-2=0
=>(x-2)(2x^2-4x+1)=0
=>x=2; \(x=\dfrac{4\pm\sqrt{14}}{2}\)
CH
1
10 tháng 1 2018
\(x^8+x+1\)
\(=\left(x^8+x^7+x^6\right)-\left(x^7+x^6+x^5\right)+\left(x^5+x^4+x^3\right)-\left(x^4+x^3+x^2\right)+\left(x^2+x+1\right)\)
\(=x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)
Chúc bạn học tốt!!!
3 tháng 4 2022
\(B\left(x\right)=2x^3-18x=0\)
\(\Leftrightarrow2x\left(x^2-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x^2-9=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm3\end{matrix}\right.\)
3 tháng 4 2022
Xét B(x)=0
⇒ 2x3- 18x = 0
⇒2x (x2 - 9 ) = 0
⇒\(\left\{{}\begin{matrix}2x=0\\x^2-9=0\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x=0:2\\x^2=0+9\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
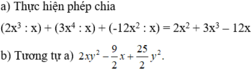
\(2x^3-12x^2+18x\)
\(=2x\left(x^2-6x+9\right)\)
\(=2x\left(x-3\right)^2\)
2x3-12x2+18x
=>2x(x2-6x+9)
=>2x(x-3)2