Cho đường tròn (O) đường kính AB. Gọi K là điểm nằm giữa A và O và H là trung điểm của KA, I là trung điểm của KB. Kẻ dây CD vuông góc với AB tại H, dâu CB cắt đường tròn (I) đường kính KB tại E.
a) Tứ giác ACKD là hình gì? Vì sao?
b) Chứng minh ba điểm D, K, E thẳng hàng
c) Chứng minh HE là tiếp tuyến của đường tròn (I).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 6 2023
OB=OC
MB=MC
=>OM là trung trực của BC
=>OM vuông góc BC tại I
góc CHO+góc CIO=180 độ
=>CHOI nội tiếp
CM
9 tháng 9 2017
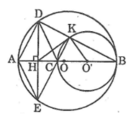
Ta có: HA = HC (gt)
AB ⊥ DE (gt)
Suy ra: HD = HE (đường kính vuông góc với dây cung)
Tứ giác ADCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Lại có: AC ⊥ DE
Suy ra tứ giác ADCE là hình thoi
CM
20 tháng 10 2018
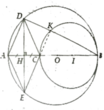
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0
CM
23 tháng 4 2019
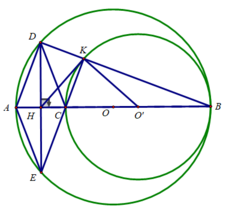
b) Dây DE của (O) vuông góc với đường kính AB
⇒ AB đi qua trung điểm của DE hay H là trung điểm của AB
Xét tứ giác ADCE có:
H là trung điểm của AB
H là trung điểm của AC
⇒ Tứ giác ADCE là hình bình hành
Lại có: AC ⊥ DE
⇒ Tứ giác ADCE là hình thoi.
1 tháng 10 2021
a: Xét (O) có
OH là một phần đường kính
DE là dây
OH\(\perp\)DE tại H
Do đó: H là trung điểm của DE
Xét tứ giác CDAE có
H là trung điểm của đường chéo DE
H là trung điểm của đường chéo CA
Do đó: CDAE là hình bình hành
mà CA\(\perp\)DE
nên CDAE là hình thoi