Cho các điện trở: R1= 1Ω, R2=\(\dfrac{1}{2}\)Ω, R3=\(\dfrac{1}{3}\) Ω,...., R2021= \(\dfrac{1}{2021}\)Ω mắc song song với nhau. Tính điện trở tương đương của đoạn mạch
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
9 tháng 11 2021
Bài 3:
a. Cần mắc vào HĐT 220V để sáng bình thường.
b. \(I=P:U=1100:220=5A\)
c. \(A=Pt=1100.2.30=66000\)Wh = 66kWh = 237 600 000J
d. \(R=p\dfrac{l}{S}\Rightarrow l=\dfrac{R.S}{p}=\dfrac{\left(220:5\right).0,45.10^{-6}}{1,10.10^{-6}}=18\left(m\right)\)
Bài 4:
a. \(Q_{toa}=A=I^2Rt=2,4^2\cdot120\cdot25=17280\left(J\right)\)
b. \(Q_{thu}=mc\Delta t=1.4200.75=315000\left(J\right)\)
\(H=\dfrac{Q_{thu}}{Q_{toa}}100\%=\dfrac{17280}{315000}100\%\approx5,5\%\)
N
9 tháng 11 2021
Baì 1:
a. \(R=R1+R2=4+6=10\Omega\)
\(I=I1=I2=U:R=18:10=1,8A\left(R1ntR2\right)\)
b. \(R1nt\left(R2\backslash\backslash\mathbb{R}3\right)\)
\(R'=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=4+\left(\dfrac{6.12}{6+12}\right)=8\Omega\)
\(I'=U:R'=18:8=2,25A\)
Bài 2:
a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{15.10}{15+10}=6\Omega\)
b. \(U=U1=U2=18V\left(R1\backslash\backslash\mathbb{R}2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=18:15=1,2A\\I2=U2:R2=18:10=1,8A\end{matrix}\right.\)
AN
2 tháng 10 2021
R12=\(\dfrac{R1.R2}{R1+R2}=\dfrac{20.100}{20+100}=\dfrac{50}{3}\)ôm
Rtđ=\(\dfrac{R12.R3}{R12+R3}=160ôm\)
28 tháng 9 2021
\(R1//R2\Rightarrow Rtd=\dfrac{R1R2}{R1+R2}=24\Omega\Rightarrow Im=\dfrac{U}{Rtd}=\dfrac{12}{24}=0,5A\)
\(\Rightarrow R2//\left(R1ntR3\right)\Rightarrow Im=\dfrac{U}{\dfrac{R2\left(R1+R3\right)}{R2+R1+R3}}=0,4A\)
13 tháng 10 2021
Do mắc song song nên:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}\)\(\Rightarrow1=\dfrac{1}{\dfrac{1}{3}+\dfrac{1}{R_2}}\)
\(\Rightarrow\dfrac{1}{3}+\dfrac{1}{R_2}=1\Rightarrow\dfrac{1}{R_2}=\dfrac{2}{3}\Rightarrow R_2=1,5\left(\Omega\right)\)
N
30 tháng 10 2021
\(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=10+\left(\dfrac{20.30}{20+30}\right)=22\left(\Omega\right)\)
30 tháng 10 2021
Điện trở tương đương:
\(R_{tđ}=R_1+\dfrac{R_2\cdot R_3}{R_2+R_3}=10+\dfrac{20\cdot30}{20+30}=22\Omega\)
VT
5 tháng 4 2017
Đáp án B
Điện trở tương đương của 3 điện trở song song:
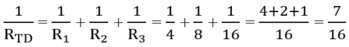
Vậy R Đ = 16 / 7
22 tháng 10 2021
\(R_1ntR_2\)
a) \(R_{tđ}=R_{12}=R_1+R_2=10+15=25\Omega\)
b) \(I_1=I_2=I_m=\dfrac{U}{R_{tđ}}=\dfrac{7,5}{25}=0,3A\)
\(\Rightarrow\left\{{}\begin{matrix}U_1=I_1\cdot R_1=0,3\cdot10=3V\\U_2=7,5-3=4,5V\end{matrix}\right.\)
c) Nếu mắc thêm R3=5Ω thì \(\left(R_1ntR_2\right)//R_3\)
\(R=\dfrac{R_3\cdot R_{12}}{R_3+R_{12}}=\dfrac{5\cdot25}{5+25}=\dfrac{25}{6}\Omega\)
\(I=\dfrac{7,5}{\dfrac{25}{6}}=1,8A\)
\(U_3=U_{12}=U_m=7,5V\)
\(\Rightarrow\) \(I_3=\dfrac{7,5}{5}=1,5A\) \(\Rightarrow I_1=I_2=I_{12}=1,8-1,5=0,3A\)
19 tháng 9 2021
R1//R2//R3
a,\(\Rightarrow\dfrac{1}{RTt}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}\Rightarrow Rtd=12,5\Omega\)
b,\(\Rightarrow\left\{{}\begin{matrix}I1=\dfrac{37,5}{25}=1,5A\\I2=\dfrac{37,5}{50}=0,75A\\I3=\dfrac{37,5}{50}=0,75A\end{matrix}\right.\)\(\Rightarrow Im=\dfrac{37,5}{Rtd}=3A\)
N
16 tháng 11 2021
\(R=\dfrac{R1\cdot R2}{R1+R2}=\dfrac{15\cdot10}{15+10}=6\Omega\)
\(U=U1=U2=18V\)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=18:15=1,2A\\I2=U2:R2=18:10=1,8A\end{matrix}\right.\)
\(R'=\dfrac{R1\cdot\left(R2+R3\right)}{R1+R2+R3}=\dfrac{15\cdot\left(10+5\right)}{15+10+5}=7,5\Omega\)
\(\Rightarrow I'=U:R'=18:7,5=2,4A\)
16 tháng 11 2021
a)\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{15\cdot10}{15+10}=6\Omega\)
b)\(U_1=U_2=U_m=18V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{18}{15}=1,2A\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{18}{10}=1,8A\)
c)\(R_1//\left(R_2ntR_3\right)\)
Bạn tự vẽ mạch nhé, mình viết cấu tạo mạch rồi.
\(R_{23}=R_2+R_3=10+5=15\Omega\)
\(R_{tđ}=\dfrac{R_{23}\cdot R_1}{R_{23}+R_1}=\dfrac{15\cdot15}{15+15}=7,5\Omega\)
\(I_m=\dfrac{U_m}{R_{tđ}}=\dfrac{18}{7,5}=2,4A\)
\(\Rightarrow\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+....+\dfrac{1}{R2021}\)
\(\Rightarrow\dfrac{1}{Rtd}=\dfrac{1}{1}+\dfrac{1}{\dfrac{1}{2}}+\dfrac{1}{\dfrac{1}{3}}+....+\dfrac{1}{\dfrac{1}{2021}}\)
\(\Rightarrow\dfrac{1}{Rtd}=1+2+3+....+2021\)
\(A=1+2+3+....+2021\)
\(A=2021+2020+2019+...+1\)
\(\Rightarrow2A=2022+2022+...+2022\)(co 2021 so 2022)
\(\Rightarrow2A=2022.2021\Rightarrow A=\dfrac{2022.2021}{2}=2043231\)
\(\Rightarrow\dfrac{1}{Rtd}=A\Rightarrow Rtd=4,89.10^{-7}\left(\Omega\right)\)