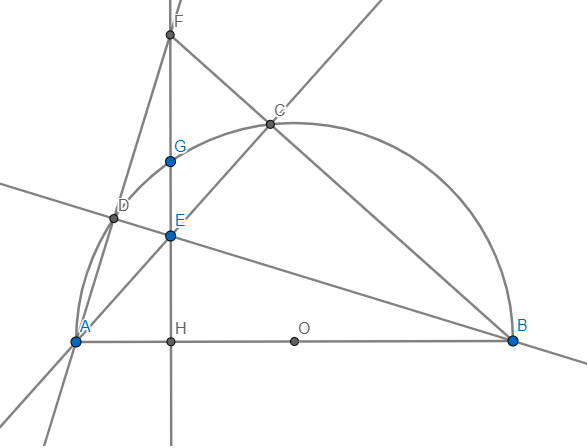
Cho nửa đường tròn (O) đường kính AB. Trên các bán kính OA và OB lần lượt lấy các điểm E và F sao cho OE=OF. Từ E và F vẽ hai đường thẳng song song với nhau cắt nửa đường tròn tại C, D. Cho AB=10cm, CD=6cm. Tính \(S_{CDFE}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi FO cắt (O) tại G khác F. Dễ dàng chứng minh \(\Delta\)DOF = \(\Delta\)COG (c.g.c) => ^OFD = ^OGC
=> DF // CG. Mà DF // CE nên E,C,G thẳng hàng (Tiên đề Euclid). Khi đó ^FEG chắn nửa đường tròn (O)
=> EF vuông góc với CE và DF. Từ đây \(S_{CEF}+S_{DEF}=\frac{EF\left(CE+DF\right)}{2}\)(1)
Dễ thấy OI là đường trung bình của hình thang CEFD (CE // DF) => \(OI=\frac{CE+DF}{2}\)(2)
Từ (1) và (2) suy ra \(S_{CEF}+S_{DEF}=EF.OI\)(đpcm).

Lời giải:
Kẻ đường kính $CT$ của $(O)$ thì $O$ là trung điểm $CT$
Xét tứ giác $CNTM$ có 2 đường chéo $CT,MN$ cắt nhau tại trung điểm $O$ của mỗi đường nên $CNTM$ là hình bình hành.
$\Rightarrow CM\parallel NT$. Mà CM\parallel DN$ nên $DN\parallel NT$ hay $D,N,T$ thẳng hàng.
Ta có: $\widehat{CDN}=\widehat{CDT}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow CD\perp DN$. Mà $DN\parallel MC$ nên $CD\perp MC$ (đpcm)

a) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle ACB=90\)
\(\Rightarrow\angle FDE+\angle FCE=90+90=180\Rightarrow ECFD\) nội tiếp
b) GH cắt AD tại F'.F'B cắt AE tại C'
Ta có: \(\left\{{}\begin{matrix}F'H\bot AB\\BD\bot AF'\end{matrix}\right.\Rightarrow E\) là trực tâm \(\Delta F'AB\Rightarrow AE\bot F'B\Rightarrow AC'\bot F'B\)
mà AB là đường kính \(\Rightarrow C'\in\left(O\right)\Rightarrow C\equiv C'\Rightarrow F'\equiv F\Rightarrow\) đpcm