Cho hình vuông ABCD, có E nằm trên cạnh BC, tia phân giác góc ABE cắt AD tại F.
CM : AF + EC = BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 12 2018
trên tia đối của AD lấy N sao cho AN = CE
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
6 tháng 8 2015
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
li-ke cho minhf nhes bn Nguyễn Thị Thùy Trang
16 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
=>góc ABD=góc EBD
=>BD là phân giác của góc ABE
b: BA=BE
DA=DE
=>BD là trung trực của AE
TA
17 tháng 12 2017
CM AB=AF
Xét tam giác ABE vuông tại E và tam giác AFE vuông tại E, có:
AE là cạnh chung
góc BAE= góc EAF (AD là tia phân giác của góc BAC)
=>tam giác ABE= tam giác AFE (cạnh góc vuông_góc nhọn kề)
=>AB=AF (2 cạnh tương ứng)
CM: AD là đường phân giác của góc BDF
Xét tam giác ABD và tam giác AFD, có
AD là cạnh chung
AB=AF (cmt)
góc BAD= góc FAD ( AD là tia phân giác của gócBAC)
=> Tam giác ABD= tam giác AFD (c-g-c)
=>Góc BDA= góc FDA (2 góc tương ứng)
=>AD là đường phân giác của góc BDF
13 tháng 11 2021
tham khảo
Trên tia đối tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (*)
Xét ∆ ABK và ∆ CBM:
AB = CB (gt)
ˆA=ˆC=900
AK = CM (theo cách vẽ)
Do đó: ∆ ABK = ∆ CBM (c.g.c)
⇒ˆB1=ˆB4
(1)
ˆKBC=900–ˆB1
(2)
Trong tam giác CBM vuông tại C.
ˆM=900–ˆB4
(3)
Từ (1), (2) và (3) suy ra: ˆKBC=ˆM
(4)
ˆKBC=ˆB2+ˆB3
mà ˆB1=ˆB2
(gt)
ˆB1=ˆB4
(chứng minh trên)
Suy ra: ˆB2=ˆB4⇒ˆB2+ˆB3=ˆB3+ˆB4
hay ˆKBC=ˆEBM
(5)
Từ (4) và (5) suy ra: ˆEBM=ˆM
⇒ ∆ EBM cân tại E ⇒ EM = BE (**)
Từ (*) và (**) suy ra: AK + CE = BE
18 tháng 4 2021
a/ Xét tg ABD và tg EBD có:
BD chung
AB = BE (gt)
góc ABD = góc EBD ( BD là pg góc B)
=> tg ABD = tg EBD (c-g-c)
=> \(\left\{{}\begin{matrix}\text{AD = DE (2 cặp cạnh tương ứng)}\\\text{góc BAD = góc BED (2 cặp góc tương ứng)}\end{matrix}\right.\)
mà góc BAD = 90 ( tg ABC vuông tại A)
=> góc BED = 90
=> DE vuông góc BC
CM
1 tháng 6 2019
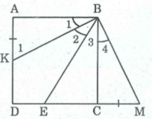
Trên tia đối của tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (1)
Xét ∆ ABK và ∆ CBM, ta có:
AB = CB (gt)
∠ A = ∠ C = 90 0
AK = CM (theo cách vẽ)
Suy ra: ∆ ABK = ∆ CBM (c.g.c)
⇒ ∠ B 1 = ∠ B 4 (2)
Lại có: ∠ B 1 = ∠ B 2 ( do BK là tia phân giác của ABE)
Suy ra: ∠ B 1 = ∠ B 2 = ∠ B 4
Mà ∠ (KBC) = 90 0 - ∠ B 1 (3)
Tam giác CBM vuông tại C nên: ∠ M = 90 0 - ∠ B 4 (4)
Từ (2), (3) và (4) suy ra: ∠ (KBC) = ∠ M (5)
Hay ∠ B 2 + ∠ B 3 = ∠ M
⇒ ∠ B 4 + ∠ B 3 = ∠ M( vì ∠ B 2 = ∠ B 4 )
Hay: ∠ (EBM) = ∠ M
⇒ ∆ EBM cân tại E ⇒ EM = BE. (6)
Từ (1) và (6) suy ra: AK + CE = BE.