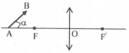
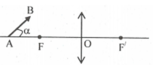
Cho vật phẳng AB, AB ⊥ △, tiêu cự f, AB > f.
a) Vẽ ảnh AA'
b) Cho OA = d; OA' = d' . Chứng minh \(\dfrac{A'B'}{AB}\) = \(\dfrac{d'}{d}\) và \(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Dựng ảnh thật A’B’ của AB bằng cách sử dụng 2 tia tới:
+ Qua O kẻ trục phụ song song với AB. Từ F’ kẻ đường vuông góc với trục chính cắt trục phụ tại F ' p
+ Kẻ tia ABI đi trùng vào AB, tia khúc xạ tại I qua tiêu điểm phụ F ' p cắt trục chính tại điểm A'

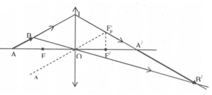
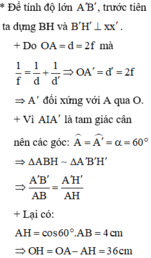


– Với d 1 = 12cm: ảnh ảo là : d 1 ’ = -30cm
- Với d 2 = -30cm: vật ảo là d 2 ’ = 12cm (không xét).
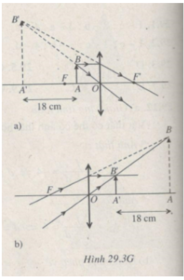



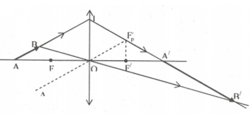

a) O B A I F F' B' A' Genius Kronos Huy d d'
b) Ta có ΔBOA∼ΔB'OA'
=>\(\dfrac{BA}{AO}=\dfrac{B'A'}{OA'}\)
=>\(\dfrac{h}{d}=\dfrac{h'}{d'}\Rightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\) (1)
Lại có ΔIOF'∼ΔB'A'F'
=>\(\dfrac{IO}{A'B'}=\dfrac{OF'}{A'F'}\)
mà IO=AB=h
A'F'=A'O-OF'=d'-f'
=>\(\dfrac{h}{h'}=\dfrac{f}{d'-f'}\) (2)
Từ (1) và (2)
=>\(\dfrac{d}{d'}=\dfrac{f}{d'-f'}\)
=>dd'-df'=d'f
Chia mỗi vế cho dd'f
(f=f ')
=>\(\dfrac{1}{f}-\dfrac{1}{d'}=\dfrac{1}{d}\)
=>\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
đpcm
đ? nào nằm trên trục chính??
A hay B ??