tìm hệ só của x^2 trong khai triển của biểu thức (2x-1)^2(3x-2)(4x+3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hệ số của x trong khai triển đã cho là: \(1-2+3-4+...+2017-2018=\left(-1\right)+\left(-1\right)+...+\left(-1\right)=-1009\).

Ta có ( 2 + 3 x ) 9 = ∑ k = 0 9 C 9 k 2 9 − k ( 3 x ) k = ∑ k = 0 9 C 9 k 2 9 − k 3 k . x k
⇒ h ( x ) = ∑ k = 0 9 C 9 k 2 9 − k 3 k x k + 1
Số hạng chứa x 7 ứng với giá trị k thỏa mãn k +1=7
Vậy hệ số chứa x 7 là: C 9 6 2 3 3 6 = 489888 .
Chọn đáp án D

Chọn D
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa
x
5
trong A(x) là![]()
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa
x
5
trong B(x) là ![]()
Vậy hệ số của số hạng chứa x 5 trong khai triển P(x) đã cho là 240-13608 = -13368.

Chọn D
Hệ số của
x
5
trong khai triển biểu thức
x
(
1
-
2
x
)
5
là hệ số của
x
4
trong khai triển biểu thức
(
1
-
2
x
)
5
và bằng ![]() .
.
Hệ số của
x
5
trong khai triển biểu thức
x
2
(
1
+
3
x
)
10
là hệ số của
x
3
trong khai triển biểu thức
(
1
+
3
x
)
10
và bằng ![]() .
.
Vậy hệ số của x 5 trong khai triển biểu thức x ( 1 - 2 x ) 5 + x 2 ( 1 + 3 x ) 10 bằng 3240 + 80 = 3320.

15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
C18 , c19 là lm sao vậy ạ ? Mk ko hiểu 2 bài này nơi

\(C_2^2+C_3^2+...+C_n^2=C_3^3+C_3^2+C_4^2+...+C_n^2\) (do \(C_2^2=C_3^3=1\))
\(=C_4^3+C_4^2+C_5^2+...+C_n^2=C_5^3+C_5^2+...+C_n^2\)
\(=...=C_n^3+C_n^2=C_{n+1}^3\)
Do đó:
\(2C_{n+1}^3=3A_{n+1}^2\Leftrightarrow\dfrac{2.\left(n+1\right)!}{3!.\left(n-2\right)!}=\dfrac{3.\left(n+1\right)!}{\left(n-1\right)!}\)
\(\Leftrightarrow n-1=9\Rightarrow n=10\)
\(\Rightarrow P=\left(1-x-3x^3\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(-x-3x^3\right)^k\)
\(=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^k\left(x+3x^3\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^kx^i.3^{k-i}.x^{3\left(k-i\right)}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^k.3^{k-i}.x^{3k-2i}\)
Ta có: \(\left\{{}\begin{matrix}0\le i\le k\le10\\i;k\in N\\3k-2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;2\right);\left(4;4\right)\)
Hệ số: \(C_{10}^2C_2^1\left(-1\right)^2.3^1+C_{10}^4C_4^4.\left(-1\right)^4.3^0=...\)

\(\Rightarrow he-so:\left[{}\begin{matrix}C^9_{10}C^1_9\left(-3\right)^{10-9}\left(-1\right)=270\\C^{10}_{10}C^4_{10}\left(-3\right)^{10-10}.\left(-1\right)^4=210\end{matrix}\right.\)

Hệ số của x5 trong khai triển x(1-2x)5 là (-2)4.C54
Hệ số của x5 trong khai triển x2(1+3x)10 là 33.C103
Do đó hệ số của x5 trong khai triển x(1-2x)5+ x2(1+3x)10 là
(-2)4.C54 + 33.C103= 3320
Chọn C
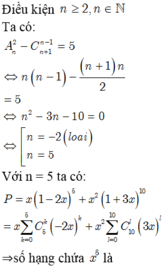

(2x-1)2 (3x-2) (4x+3) = (4x2 -4x +1) (12x2 +x -6)
= 48x4 + 4x3 - 24x2 -48x3 -4x2 +24x +12x2 +x - 6
=48x4 -44x3 -16x2+25x -6
Vậy hệ số của x2 là -16