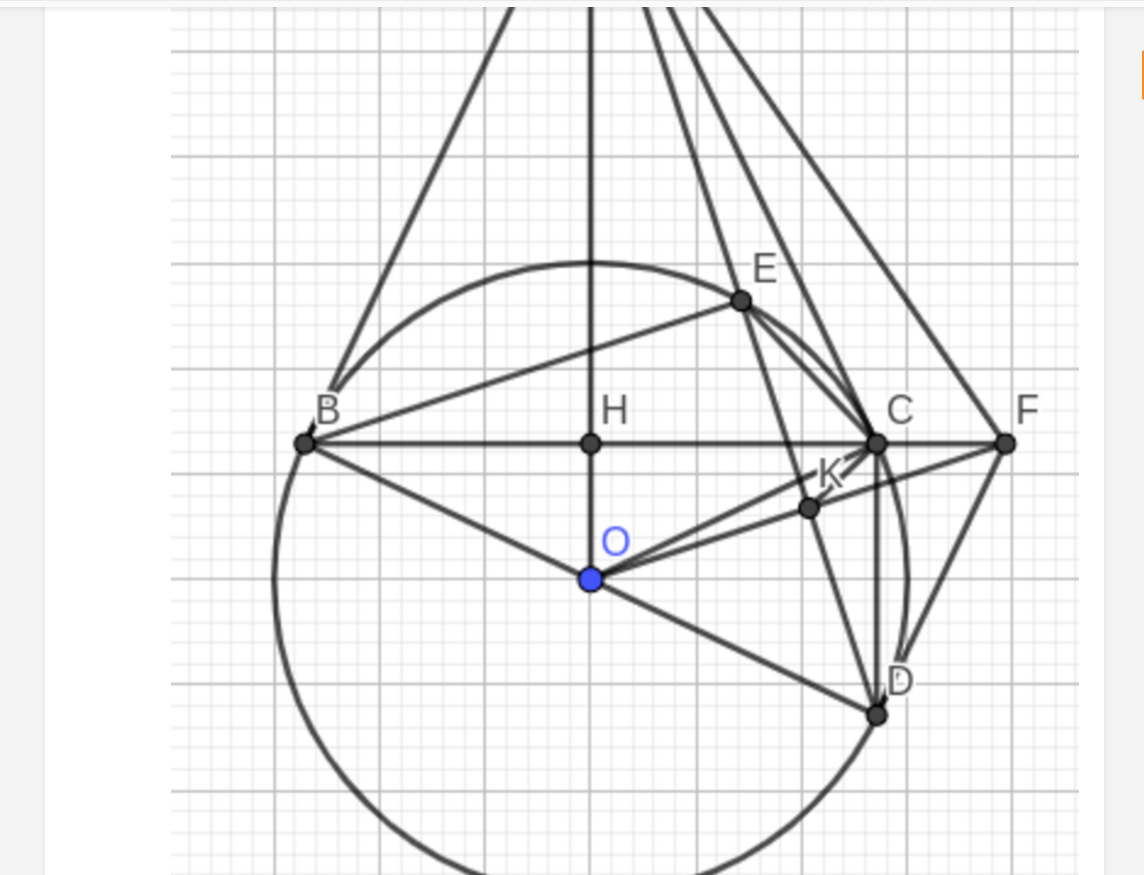
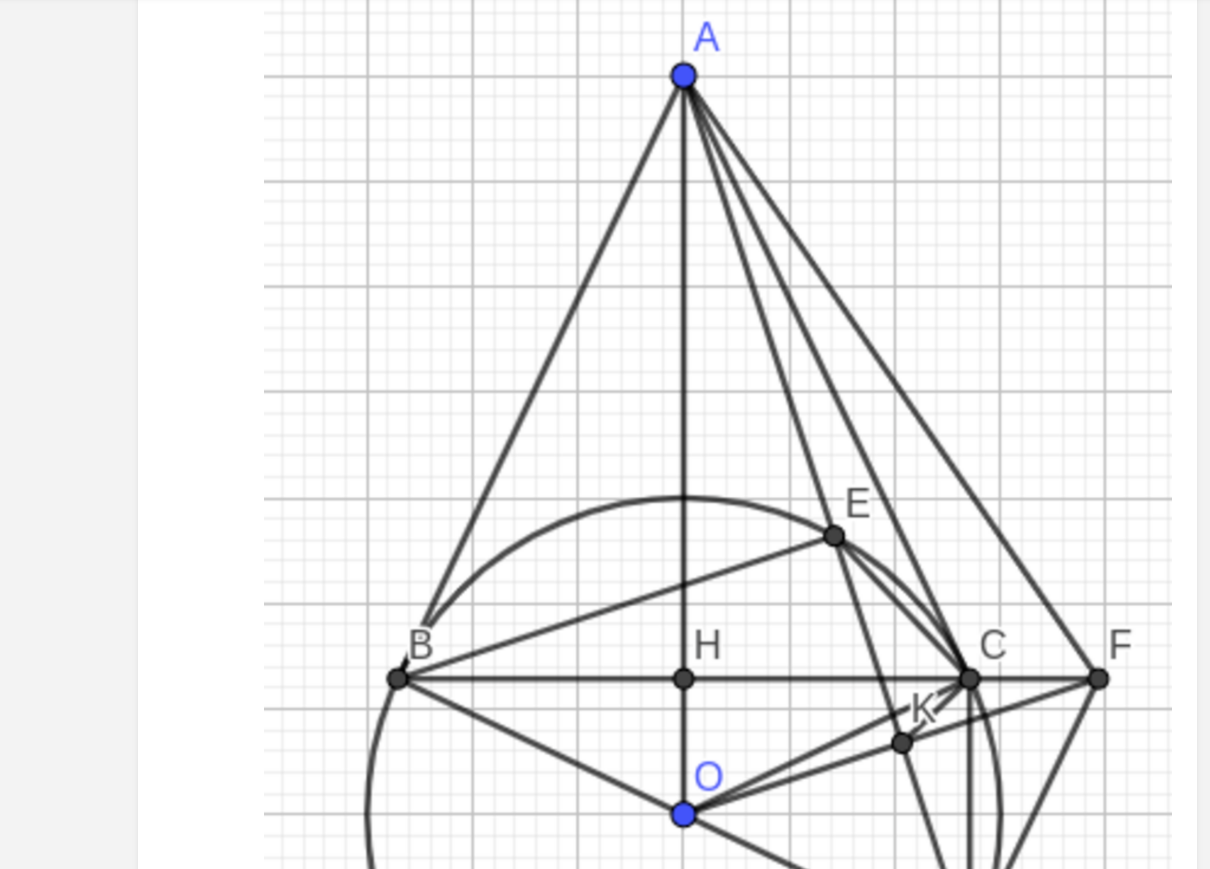
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm tiếp điểm). Gọi H là giao điểm của OA và BC.
1) Chứng minh OA vuông góc với BC tại H
2) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D). Chứng minh: AE.AD = AH.AO
3) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn (O)
4) Gọi I là trung điểm cạnh AB, qua I vẽ đường thẳng vuông góc với cạnh AO tại M và đường thẳng này cắt đường thẳng DF tại N. Chứng minh: ND = NA