Cho hình vuông ABCD, trên AB, AD lần lượt lấy các điểm M, K sao cho AM=AK. Vẽ điểm E thuộc đoạn thẳng MD sao cho \(\widehat{AKE}=\widehat{DCE}\). Tính số đo \(\widehat{AEM}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2021
a) Vì điểm C nằm giữa hai điểm A và B nên tia OC nằm giữa hai tia OA và OB
\(\Leftrightarrow\widehat{AOC}+\widehat{BOC}=\widehat{AOB}\)
\(\Leftrightarrow\widehat{BOC}+30^0=60^0\)
hay \(\widehat{BOC}=30^0\)
Vậy: \(\widehat{BOC}=30^0\)
21 tháng 1 2020
Hình vẽ bạn tự vẽ nha
Trước hết chứng minh :(tự chứng minh lun)
Cho tam giác ABC vuông cân tại A . Chứng minh \(\sqrt{2}\cdot AB=BC\)(*)
Xét tam giác KDM và tam giác IEM ta có:
KM=MI (gt)
KMD= IME (gt);
MD=ME (gt);
=> tam giác KDM = tam giác IEM (c.g.c);
=> KD= EI (tương ứng);
Lại có NMP=90 (gt) => NMK+ KMP=90
=> IME+ KMP =90 => IMK =90 mà KM=MI
=> tam giác KMI vuông cân tại M
Xét tam giác NMP vuông cân tại M có MNH=45 mà MHN=90 (do MH là đường cao)
=>Tam giác MHN vuông cân tại H
Áp dụng (*) vào tam giác KMI vuông cân tại M và tam giác MHN vuông cân tại H ta được:
\(\hept{\begin{cases}\sqrt{2}\cdot MH=MN\\\sqrt{2}\cdot KM=KI\end{cases}}\)mà \(KM\ge MH\)
\(\Rightarrow KI\ge MN\)
Xét 3 điểm K,E,I ta có:
\(KE+EI\ge KI\)
hay \(KE+KD\ge MN\)
21 tháng 1 2020
Hoàng Nguyễn Văn Dòng thứ 5 dưới lên sai rồi mem,tự coi lại nha,không thể như thế được đâu.Tại sao \(KM\ge MH\) lại suy ra \(KI\ge MN\) được ??
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 11 2021
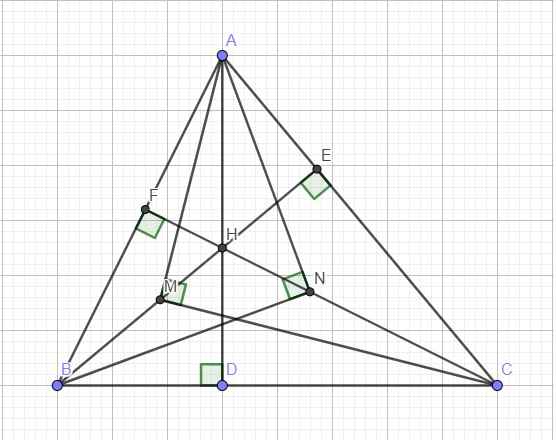
Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A
NH
0