Ai chỉ em với ạ bài III ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5
\(n_{Al_2O_3}=\dfrac{10,2}{102}=0,1\left(mol\right)\)
\(n_{HCl}=\dfrac{18,25}{36,5}=0,5\left(mol\right)\)
PTHH: Al2O3 + 6HCl --> 2AlCl3 + 3H2O
Xét tỉ lệ: \(\dfrac{0,1}{1}>\dfrac{0,5}{6}\) => Al dư, HCl hết
PTHH: Al2O3 + 6HCl --> 2AlCl3 + 3H2O
\(\dfrac{1}{12}\)<----0,5------->\(\dfrac{1}{6}\)----->0,25
=> \(\left\{{}\begin{matrix}m_{Al\left(dư\right)}=10,2-\dfrac{1}{12}.102=1,7\left(g\right)\\m_{AlCl_3}=\dfrac{1}{6}.133,5=22,25\left(g\right)\\m_{H_2}=0,25.18=4,5\left(g\right)\end{matrix}\right.\)
Bài 6
a) \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
\(n_{Mg}=\dfrac{4,8}{24}=0,2\left(mol\right)\)
PTHH: Mg + 2HCl --> MgCl2 + H2
0,1<-------------0,1<----0,1
=> \(n_{Mg\left(pư\right)}=0,1\left(mol\right)< 0,2\)
=> Mg dư => HCl hết
b) \(m_{MgCl_2}=0,1.95=9,5\left(g\right)\)
\(m_{Mg\left(dư\right)}=\left(0,2-0,1\right).24=2,4\left(g\right)\)

a,Đổi: 3 lít nước = 3 kg nước
Nhiệt lượng cần thiết để đun sôi 3 lít nước:
Q=m.c.Δt= 3.4200.(100-22) = 982800 (J)
b, Nhiệt lượng bếp điện cần toả:
\(H=\dfrac{Ai}{Atp}.100\%\Rightarrow Atp=\dfrac{Ai.100\%}{H}=\dfrac{982800.100\%}{85\%}=1156235,3\) (J)
Thời gian đun sôi:
Q = P.t \(\Rightarrow\) t = \(\dfrac{Q}{P}=\dfrac{1156235,3}{1200}\approx\)963,5 giây\(\approx\)16 phút
c,Đổi: 1200W = 1,2kW
Số đếm công tơ điện của bếp điện nếu sử dụng 2h trong 365 ngày: 1,2.2.365= 876 (kWh)
Số tiền phải trả:1800. 876 =15768000(đồng)

Bài 3:
a) Số học sinh nam là:
\(45\cdot\dfrac{3}{5}=27\)(bạn)
b) Tỉ số phần trăm giữa số học sinh nữ và số học sinh cả lớp là:
18:45=40%

Ai còn thức giúp em với ạ , em sẽ vào trang cá nhân của 2 người đầu tiên và tick 5 lần cho câu trả lời của người đó ạ , người thứ 3 em sẽ tick 2 lần ạ . M.n giúp em với , gấp lắm ạ !![]()
Đến sáng ngày mai ai giúp em thì ko kịp nộp bài nữa nên 12h tối nay và sáng mai em ko tick ạ . Mong m.n thoong cảm và giúp cho em với ạ

dạ cảm ơn anh hoặc chị ạ.Anh hoặc chị có thể giải thích vì sao ra vậy ko ạ?

Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
Bài IV.b.
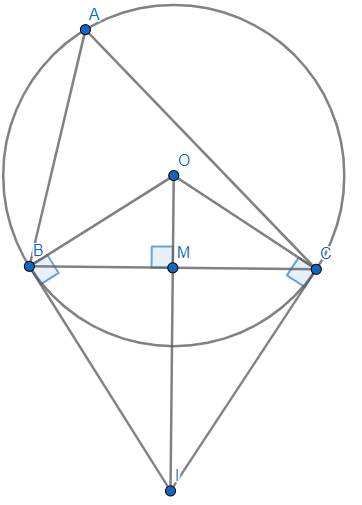
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)

1: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{2}{x-1}-\sqrt{y-2}=-1\\\dfrac{3}{x-1}+2\sqrt{y-2}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x-1}-2\sqrt{y-2}=-2\\\dfrac{3}{x-1}+2\sqrt{y-2}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{x-1}=7\\\dfrac{3}{x-1}+2\sqrt{y-2}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\2\sqrt{y-2}=9-3=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\\sqrt{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y-2=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=11\end{matrix}\right.\left(nhận\right)\)
2:
a: Phương trình hoành độ giao điểm là:
\(x^2-\left(m-2\right)x-m-4=0\)
\(\text{Δ}=\left[-\left(m-2\right)\right]^2-4\left(-m-4\right)\)
\(=m^2-4m+4+4m+16\)
\(=m^2+20>=20>0\forall m\)
=>(d) luôn cắt (P) tại hai điểm phân biệt
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(m-2\right)\right]}{1}=m-2\\x_1\cdot x_2=\dfrac{c}{a}=-m-4\end{matrix}\right.\)
\(\left|x_1+x_2\right|=\left|x_1-x_2\right|\)
=>\(\left[{}\begin{matrix}x_1+x_2=x_1-x_2\\x_1+x_2=-x_1+x_2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}-2x_2=0\\2x_1=0\end{matrix}\right.\Leftrightarrow x_1\cdot x_2=0\)
=>-m-4=0
=>m+4=0
=>m=-4



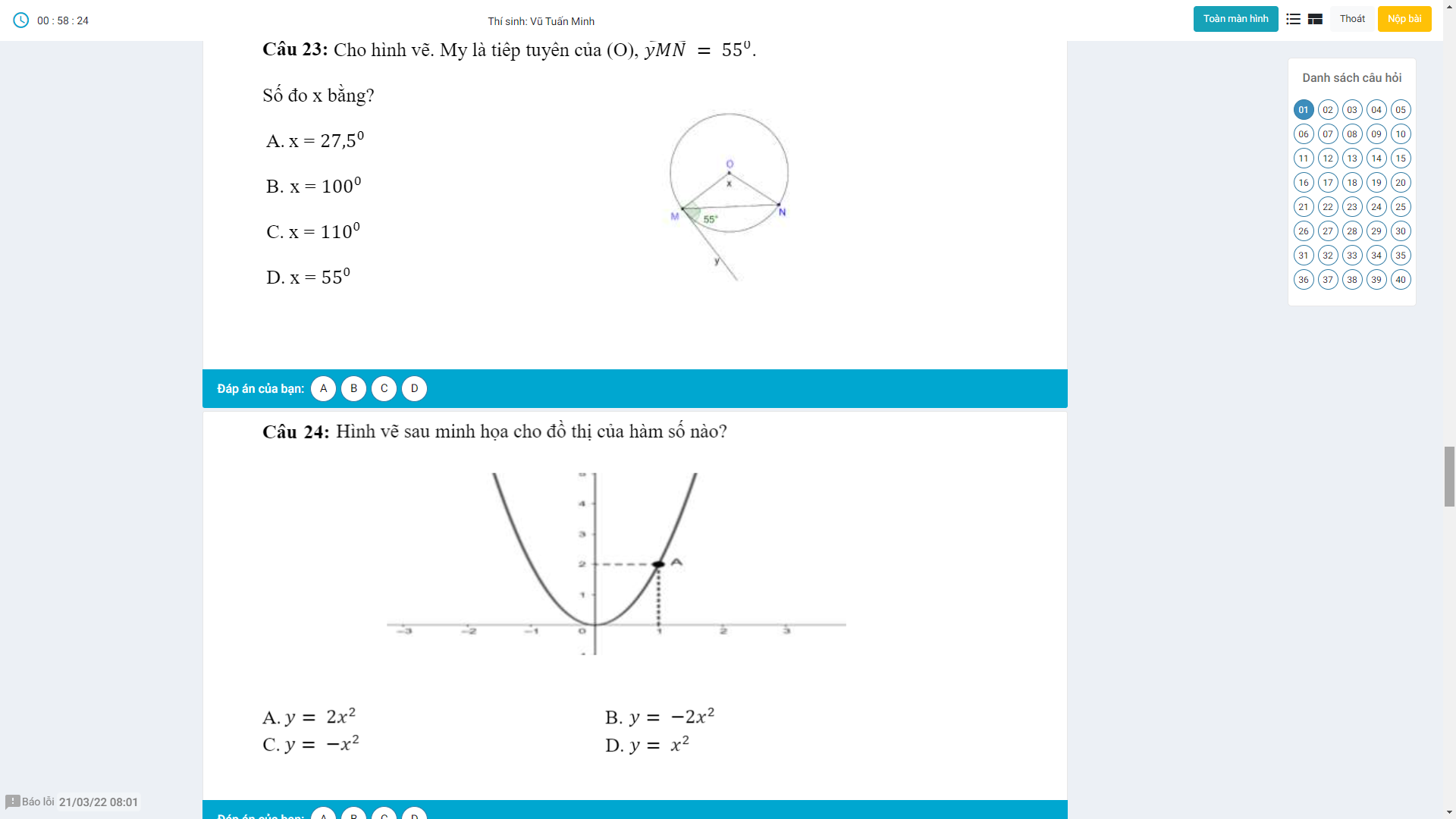

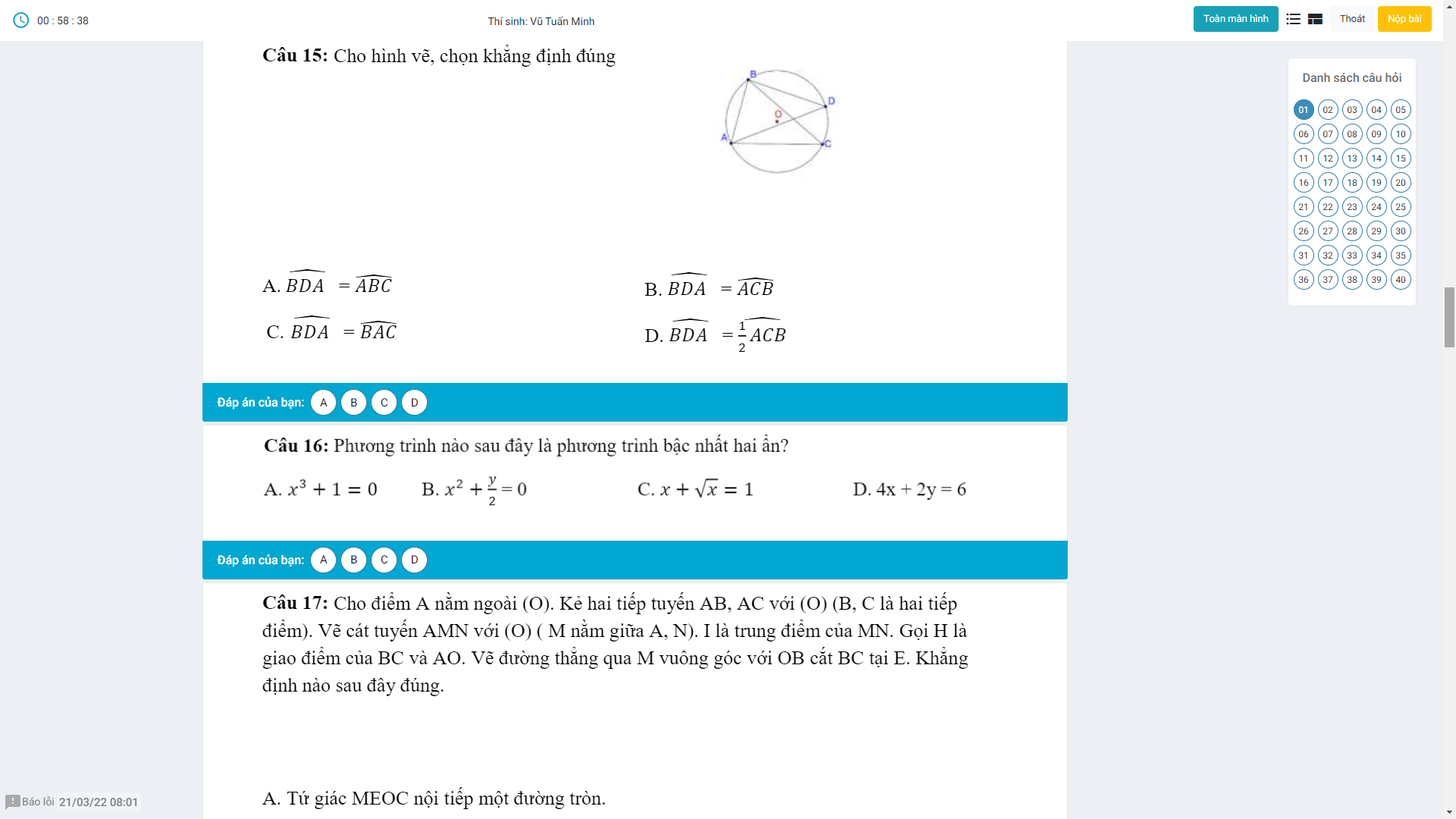

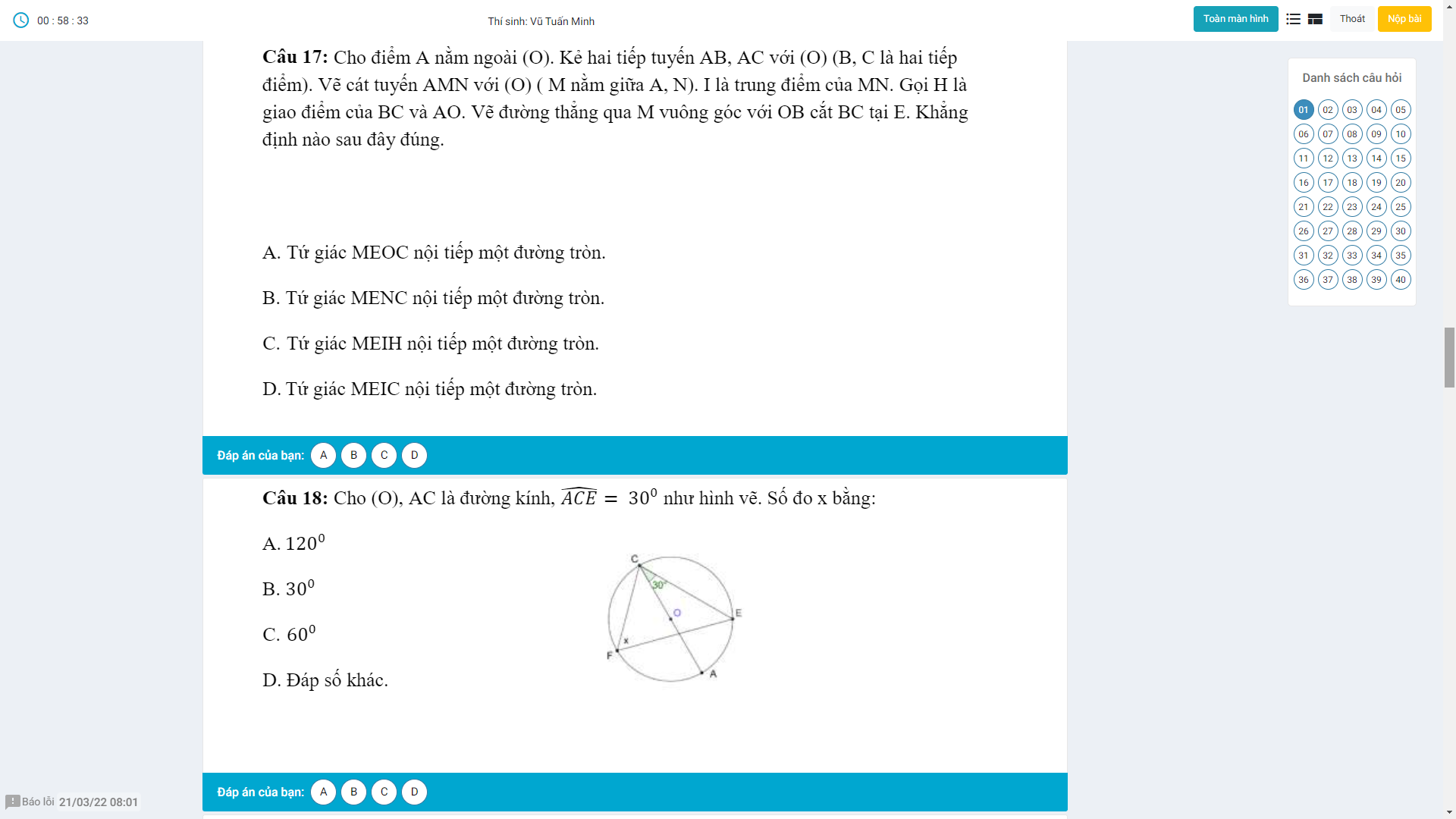
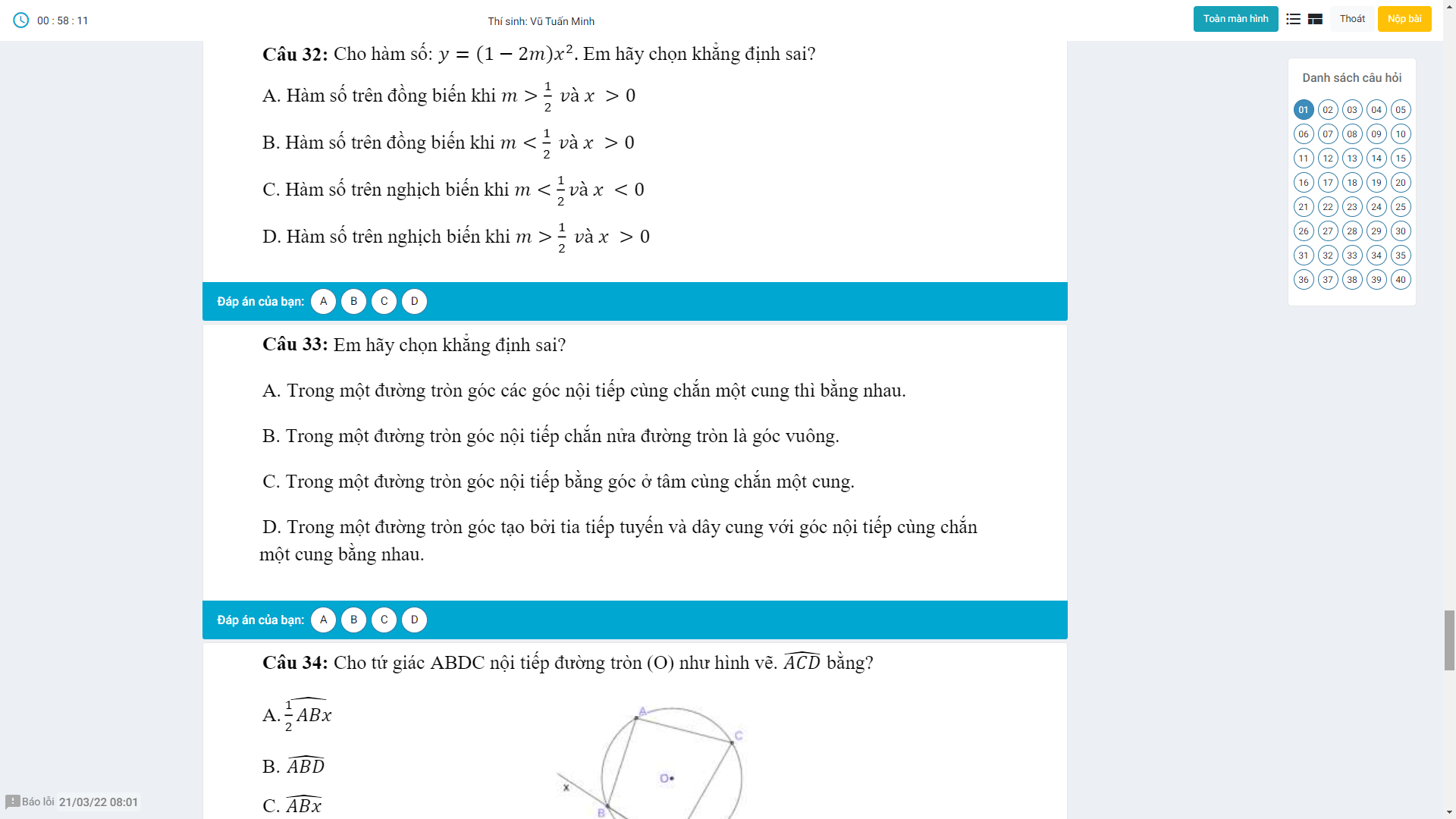
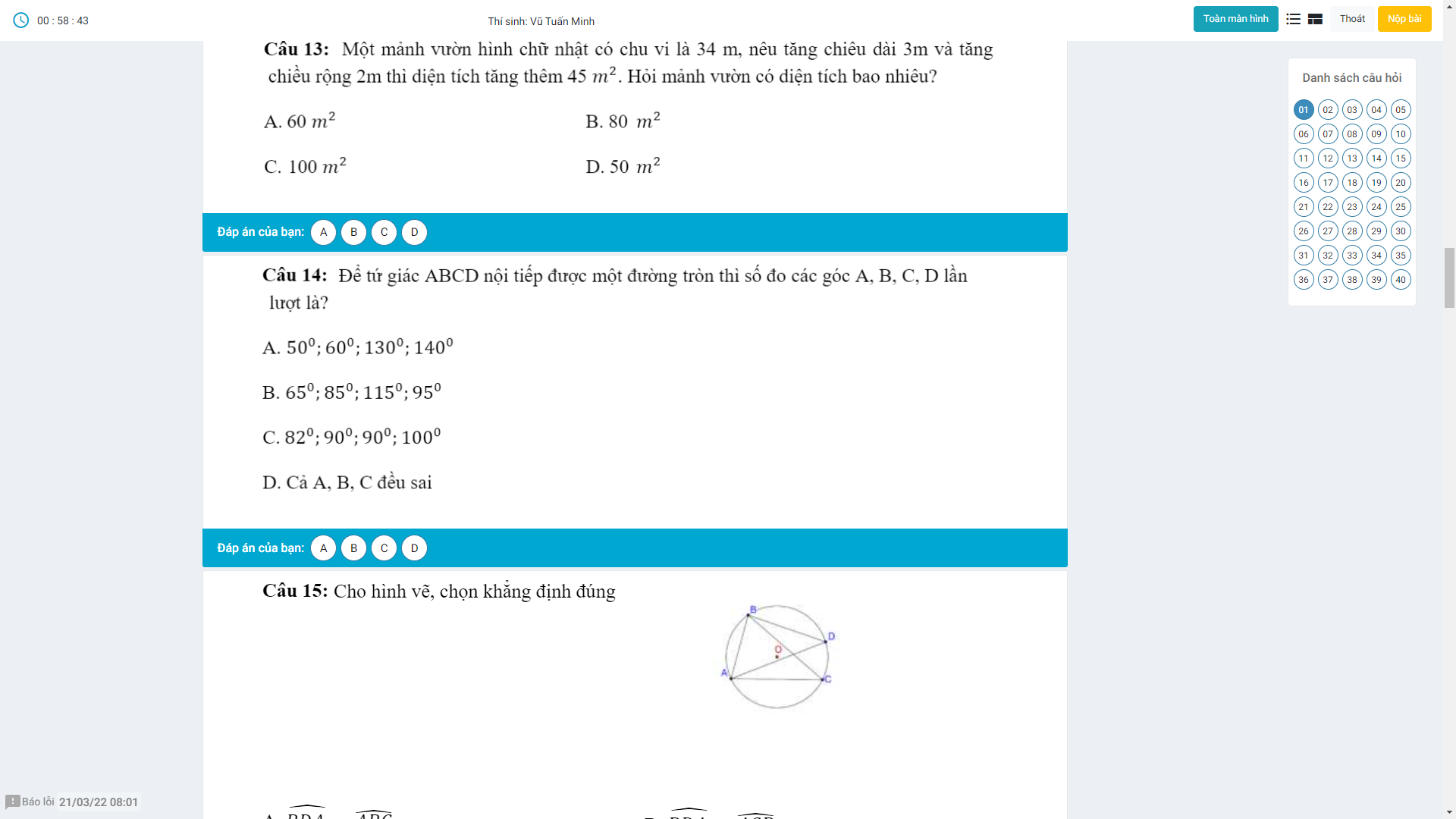
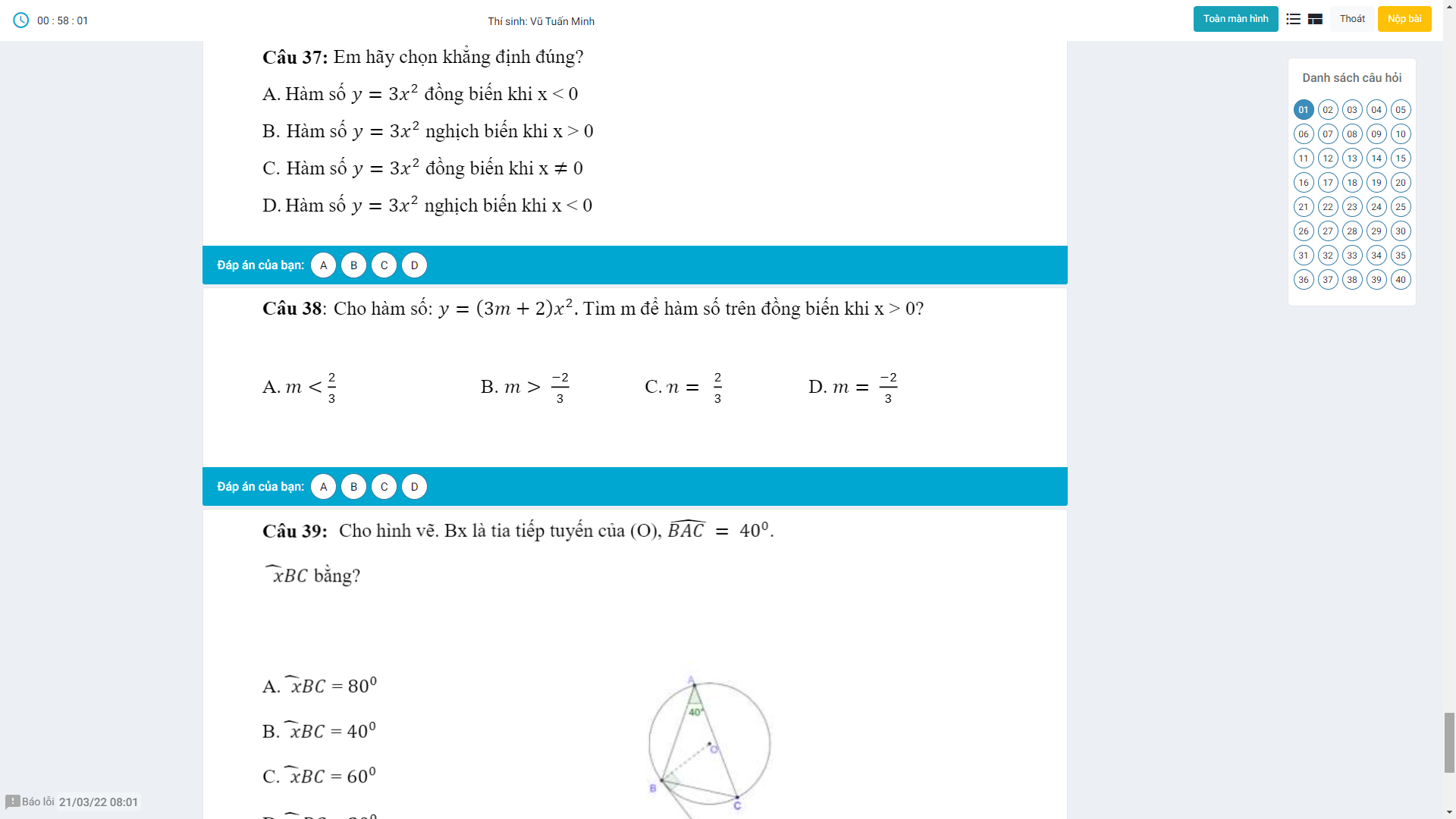

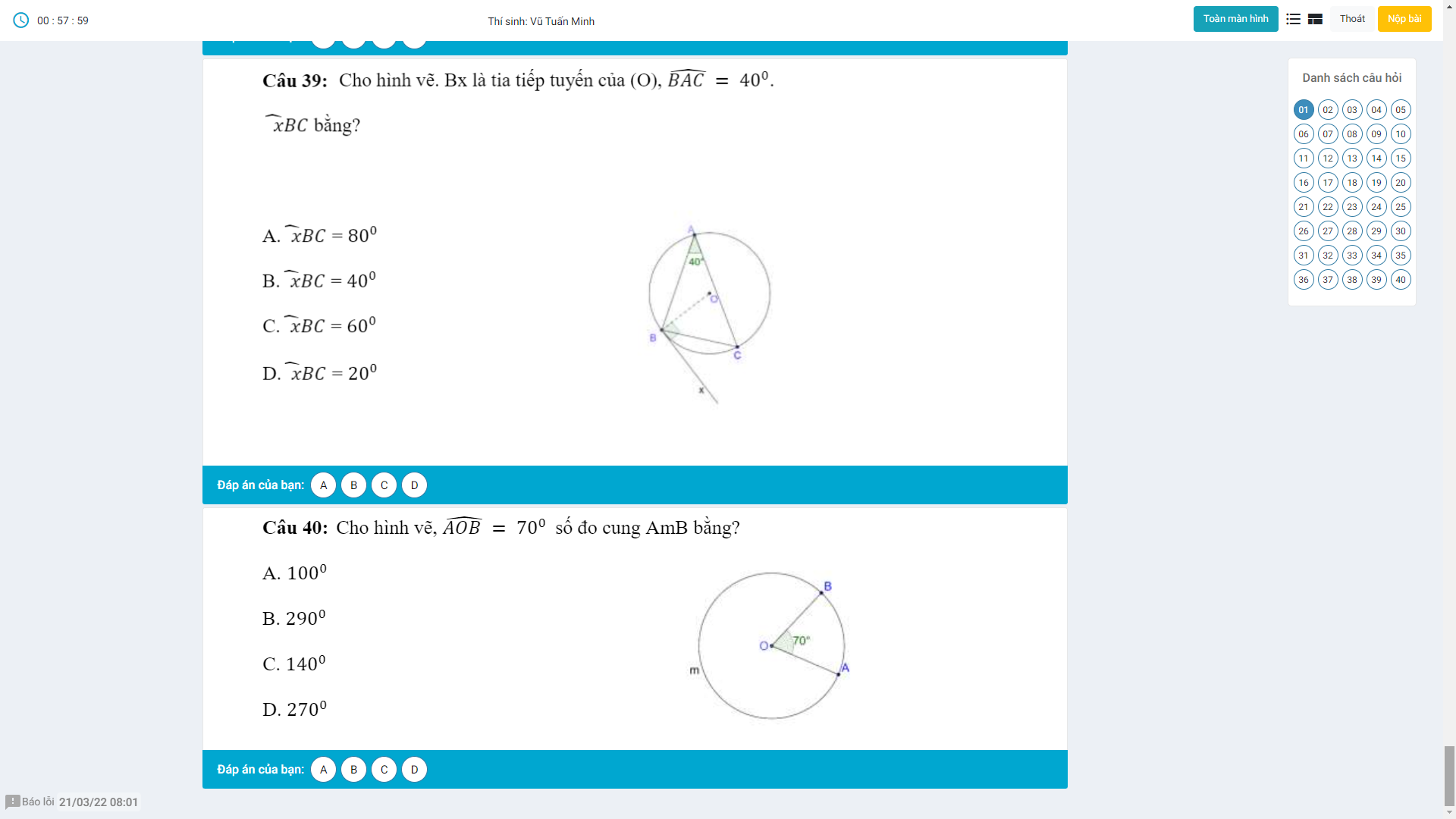
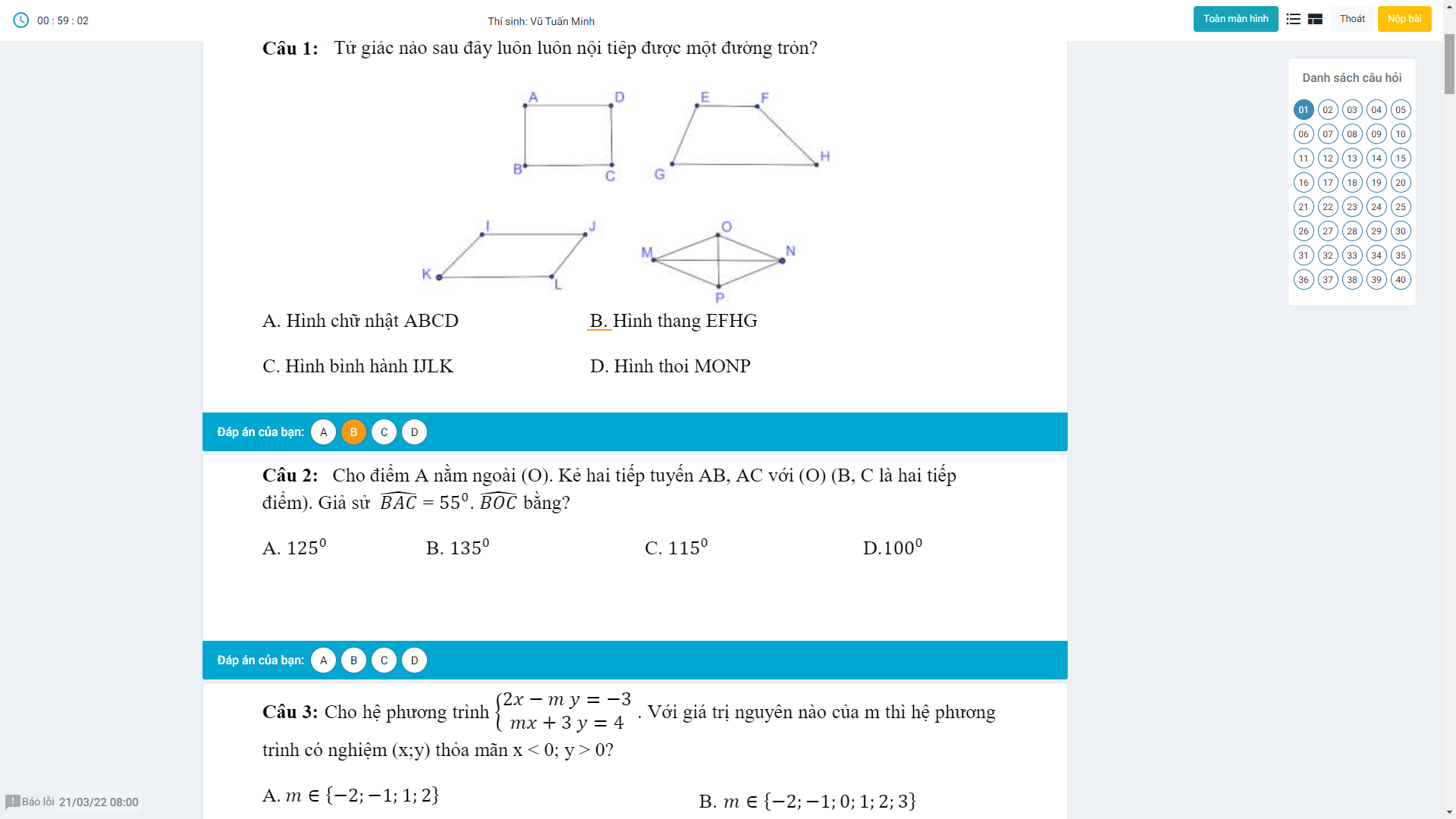

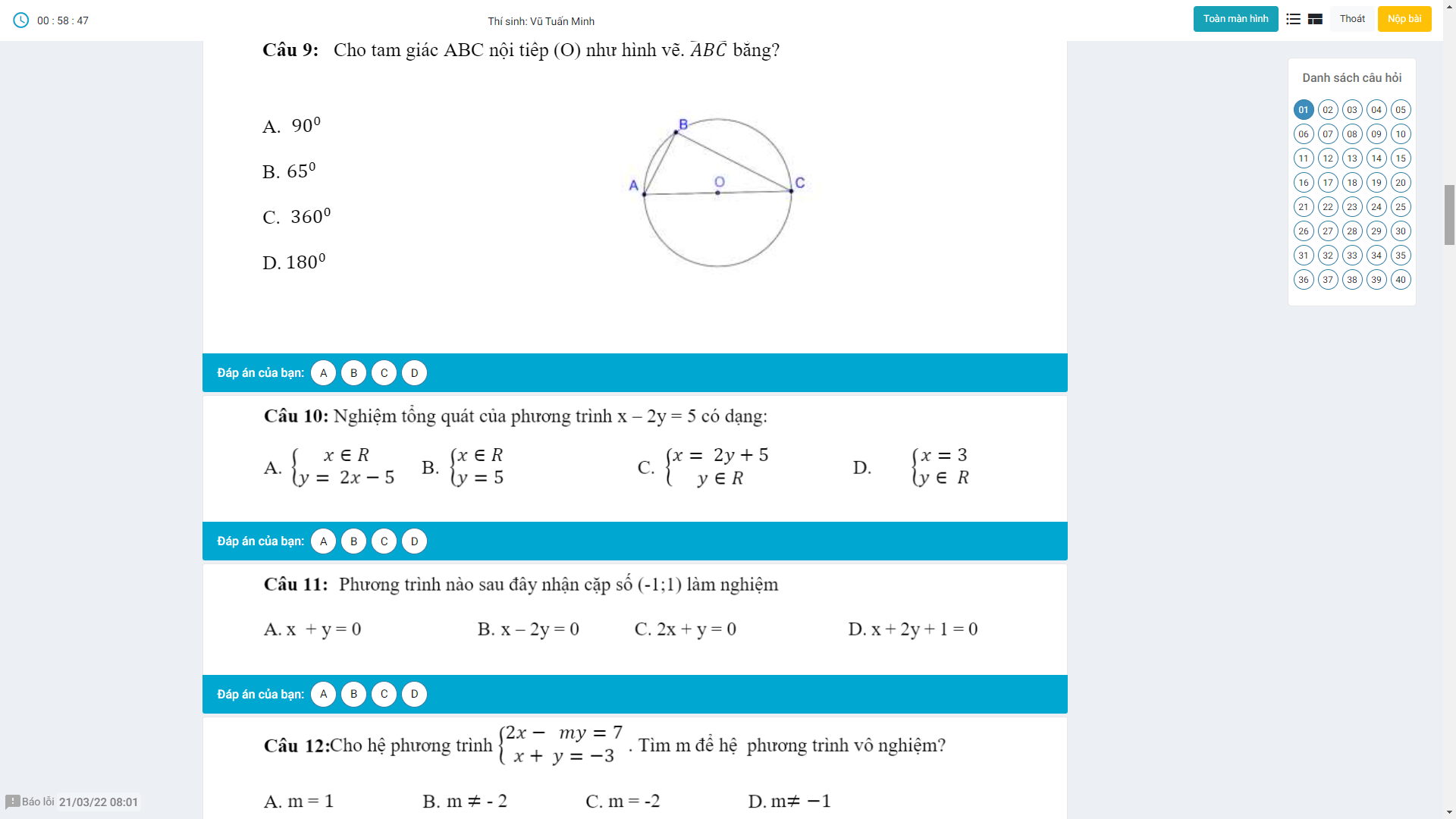
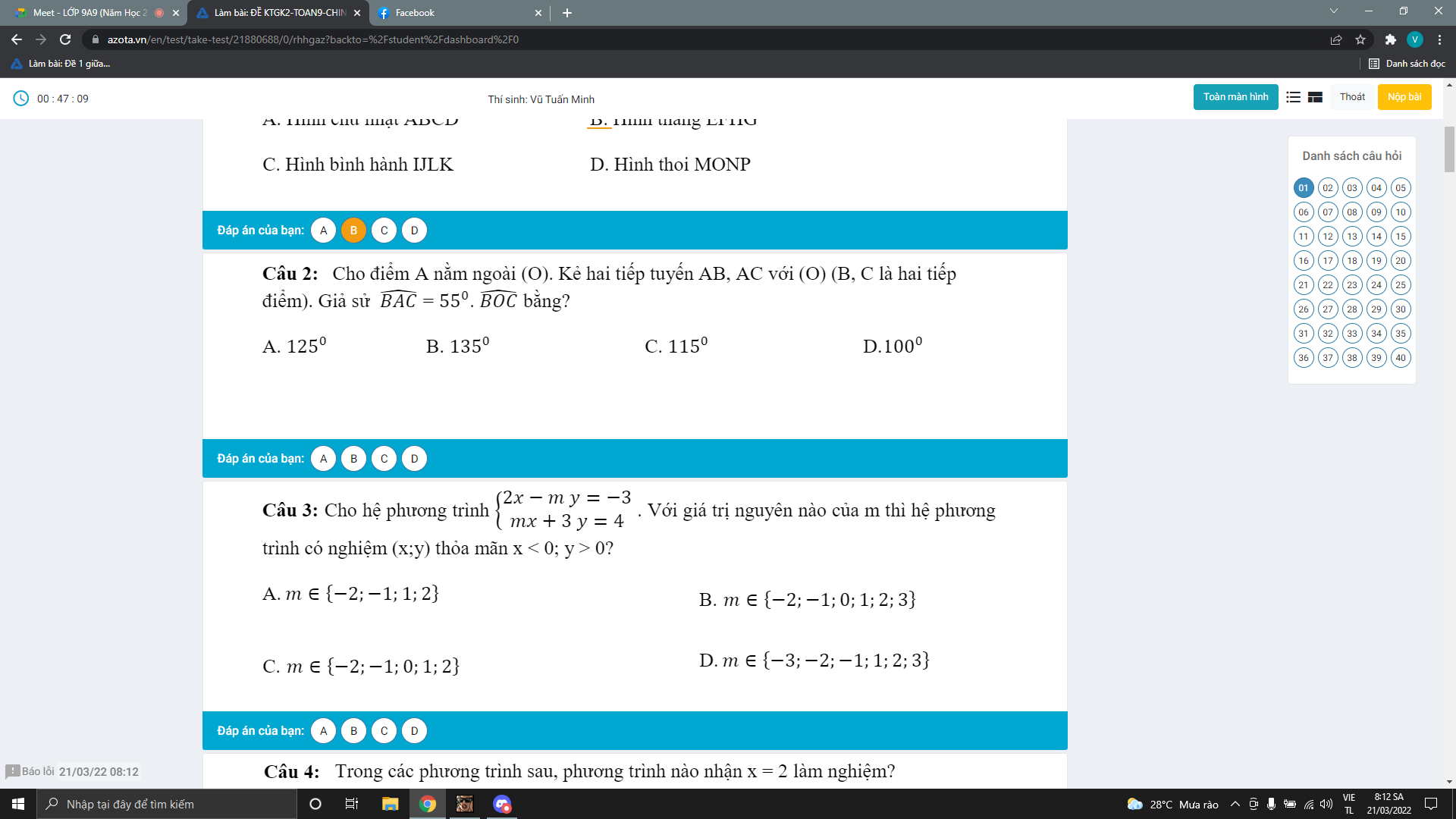


 Ai chỉ em bài này với ạ nếu rảnh thì giải thích giúp em em sẽ tick cho anh chị.Em cảm ơn anh chị nhiều ạ^^(Đây là đề kham khảo không phải đề thi đâu ạ!)
Ai chỉ em bài này với ạ nếu rảnh thì giải thích giúp em em sẽ tick cho anh chị.Em cảm ơn anh chị nhiều ạ^^(Đây là đề kham khảo không phải đề thi đâu ạ!)

1 A
2 C
3 A
4 D
5 C
6 B
7 B
8 A
9 B
10 D