Cho hình bình hành ABCD có AB = 2AD. Gọi M; N lần lượt là trung điểm của AB và CD. AN cắt DM ở P, BN cắt CM ở Q.
a, Tứ giác AMNQ là hình gì?
b, C/minh: tứ giác MPNQ là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

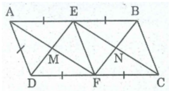
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.

Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
b: Hình bình hành AMND có AM=AD
nên AMND là hình thoi
c: Xét tứ giác ANKQ có
D là trung điểm của NQ
D là trung điểm của AK
Do đó: ANKQ là hình bình hành
a: Sửa đề; AMND
Xét tứ giác AMND có
AM//ND
AM=ND
AM=AD
Do đó: AMND là hình thoi
=>AN vuông góc với MD tại P
b: Xét tứ giác MBCN có
MB//CN
MB=CN
MB=BC
Do đó: MBCN là hình thoi
=>MC vuông góc với BN tại Q
Xét ΔMDC có
MN là đường trung tuyến
MN=CD/2
Do đó: ΔMDC vuông tại M
Xét tứ giác MPNQ có
góc MPN=góc MQN=góc PMQ=90 độ
nên MPNQ là hình chữ nhật