a) tìm x để A =x^2+2x+1/x^2-1 được xđ
b) tìm x để B= 3x^2+6x+12/x^3-8 được xđ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 3 2021
Bài 1:
c) ĐKXĐ: \(x\notin\left\{\dfrac{1}{4};-\dfrac{1}{4}\right\}\)
Ta có: \(\dfrac{3}{1-4x}=\dfrac{2}{4x+1}-\dfrac{8+6x}{16x^2-1}\)
\(\Leftrightarrow\dfrac{-3\left(4x+1\right)}{\left(4x-1\right)\left(4x+1\right)}=\dfrac{2\left(4x-1\right)}{\left(4x+1\right)\left(4x-1\right)}-\dfrac{6x+8}{\left(4x-1\right)\left(4x+1\right)}\)
Suy ra: \(-12x-3=8x-2-6x-8\)
\(\Leftrightarrow-12x-3-2x+10=0\)
\(\Leftrightarrow-14x+7=0\)
\(\Leftrightarrow-14x=-7\)
\(\Leftrightarrow x=\dfrac{1}{2}\)(nhận)
Vậy: \(S=\left\{\dfrac{1}{2}\right\}\)
25 tháng 2 2021
`a,x^3-8 ne 0`
`=>x^3 ne 8`
`=>x ne 2`
`b,2x^2+5x+3 ne 0`
`=>2x^2+2x+3x+3 ne 0`
`=>2x(x+1)+3(x+1) ne 0`
`=>(x+1)(2x+3) ne 0`
`=>x ne -1,-3/2`
`c,x^2-4 ne 0`
`=>x^2 ne 4`
`=>x ne 2,-2`
25 tháng 2 2021
a) ĐK:
\(x^3-8\ne0\\ \Leftrightarrow x\ne2\)
b) ĐK:
\(2x^2+5x+3\ne0\\ \Leftrightarrow\left[{}\begin{matrix}x\ne-1\\x\ne-\dfrac{3}{2}\end{matrix}\right.\)
c) ĐK:
\(x^2-4\ne0\\ \Leftrightarrow x\ne\pm2\)
21 tháng 12 2018
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
H
21 tháng 12 2018
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
VN
16 tháng 1 2017
a)
<=> 3x - 3 + x - 2 = 2x - 2 - x + 1
<=> 3x + x - 2x + x = -2 + 1 + 3 + 2
<=> 3x = 4
<=> x = 4/3
Các câu sau làm tương tự
29 tháng 9 2018
\(\left(3x-3\right)+\left(x-2\right)=\left(2x-2\right)-\left(x-1\right)\)
<=> \(3x-3+x-2=2x-2-x+1\)
<=> \(4x-5=x-1\)
<=> \(3x=4\)
<=> \(x=\frac{4}{3}\)
Vậy....
3 tháng 6 2021
Giải:
a) \(\dfrac{-5}{6}-x=\dfrac{7}{12}+\dfrac{-1}{3}\)
\(\dfrac{-5}{6}-x=\dfrac{1}{4}\)
\(x=\dfrac{-5}{6}-\dfrac{1}{4}\)
\(x=\dfrac{-13}{12}\)
b) \(2.\left(x-\dfrac{1}{3}\right)=\left(\dfrac{1}{3}\right)^2+\dfrac{5}{9}\)
\(2.\left(x-\dfrac{1}{3}\right)=\dfrac{1}{9}+\dfrac{5}{9}\)
\(2.\left(x-\dfrac{1}{3}\right)=\dfrac{2}{3}\)
\(x-\dfrac{1}{3}=\dfrac{2}{3}:2\)
\(x-\dfrac{1}{3}=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}+\dfrac{1}{3}\)
\(x=\dfrac{2}{3}\)
c) \(\left|2x-\dfrac{3}{4}\right|-\dfrac{3}{8}=\dfrac{1}{8}\)
\(\left|2x-\dfrac{3}{4}\right|=\dfrac{1}{8}+\dfrac{3}{8}\)
\(\left|2x-\dfrac{3}{4}\right|=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x-\dfrac{3}{4}=\dfrac{1}{2}\\2x-\dfrac{3}{4}=\dfrac{-1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{8}\\x=\dfrac{1}{8}\end{matrix}\right.\)
d) \(\dfrac{2}{3}x+\dfrac{1}{6}x=3\dfrac{5}{8}\)
\(x.\left(\dfrac{2}{3}+\dfrac{1}{6}\right)=\dfrac{29}{8}\)
\(x.\dfrac{5}{6}=\dfrac{29}{8}\)
\(x=\dfrac{29}{8}:\dfrac{5}{6}\)
\(x=\dfrac{87}{20}\)
18 tháng 11 2017
MK ko biế đúng ko nữa , sai thì ý kiến
a)
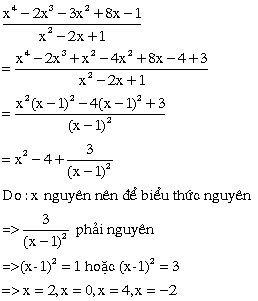
b)
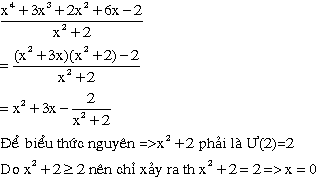
Chúc các bn hok tốt
Tham khảo nhé
A xác định \(\Leftrightarrow x^2-1\ne0\Leftrightarrow x\ne\left\{1;-1\right\}\)
B xác định \(\Leftrightarrow x^3-8\ne0\Leftrightarrow x^3\ne8\Leftrightarrow x\ne2\)