Tìm x
a:x3+6x2+9x=0
b:x3-5x2-9x+45
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
30 tháng 5 2018
45 + x 3 - 5 x 2 - 9 x = x 3 - 5 x 2 - 9 x - 45 = x 2 x - 5 - 9 x - 5 = x - 5 x 2 - 9 = x - 5 x - 3 x + 3
N
29 tháng 8 2021
\(5x^2-9x-2=0\)
\(\Delta=9^2-4.5.\left(-2\right)=121\)
\(\left[{}\begin{matrix}x_1=\dfrac{9+\sqrt{121}}{2.5}=2\\x_2=\dfrac{9-\sqrt{121}}{2.5}=-\dfrac{1}{5}\end{matrix}\right.\)
PT
1
KK
3
KV
7 tháng 6 2023
Cho n(x) = 0
5x² + 9x + 4 = 0
5x² + 5x + 4x + 4 = 0
(5x² + 5x) + (4x + 4) = 0
5x(x + 1) + 4(x + 1) = 0
(x + 1)(5x + 4) = 0
*) x + 1 = 0
x = 0 - 1
x = -1
*) 5x + 4 = 0
5x = 0 - 4
5x = -4
x = -4/5
Vậy nghiệm của đa thức n(x) là x = -1; x = -4/5
7 tháng 6 2023
Cho \(n\left(x\right)=0\) \(\Leftrightarrow5x^2+9x+4=0\)
\(\Leftrightarrow5x^2+5x+4x+4=0\)
\(\Leftrightarrow5x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Như vậy n(x) có 2 nghiệm là \(-1\) và \(-\dfrac{4}{5}\)
CM
15 tháng 7 2019
Chọn B
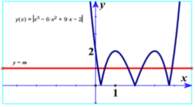
+ Đồ thị hàm số y = | x 3 - 6 x 2 + 9 x - 2 | có được bằng cách biến đổi đồ thị (C) hàm số y = x 3 - 6 x 2 + 9 x - 2
Giữ nguyên phần đồ thị (C) nằm trên trục hoành.
Lấy đồi xứng phần đồ thị của (C) phần dưới trục hoành qua trục hoành.
Xóa phần đồ thị còn lại (C) phía dưới trục hoành.
+ Số nghiệm của phương trình | x 3 - 6 x 2 + 9 x - 2 | = m là số giao điểm của đồ thị hàm số
y = | x 3 - 6 x 2 + 9 x - 2 | và đồ thị hàm số y=m. Để phương trình có 6 nghiệm phân biệt thì điều kiện cần và đủ là 0<m<2.
NL
1
8 tháng 10 2021
\(a,\Leftrightarrow2x^2-10x-2x^2-x=-11\\ \Leftrightarrow-11x=-11\Leftrightarrow x=1\\ b,\Leftrightarrow x\left(x^2-6x+9\right)=0\\ \Leftrightarrow x\left(x-3\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ c,\Leftrightarrow x\left(x-2018\right)-2017\left(x-2018\right)=0\\ \Leftrightarrow\left(x-2017\right)\left(x-2018\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=2018\end{matrix}\right.\)
Y
15 tháng 6 2023
\(6x^2-9x-4\left(2x-3\right)=0\)
\(\Leftrightarrow3x\left(2x-3\right)-4\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(3x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\3x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=3\\3x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{3}{2};\dfrac{4}{3}\right\}\)
C
1
\(x^3+6x^2+9x=0\)
\(x\left(x^2+6x+9\right)=0\)
\(x\left(x+3\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}x=0\\x=-3\end{cases}}\)
x3-5x2-9x+45=0
=>(x3-5x2)-(9x-45)=0
=>x2(x-5)-9(x-5)=0
=>(x2-9)(x-5)=0
=>x2-9=0 =>x2=9 => x=3;-3
x-5=0 =>x=5