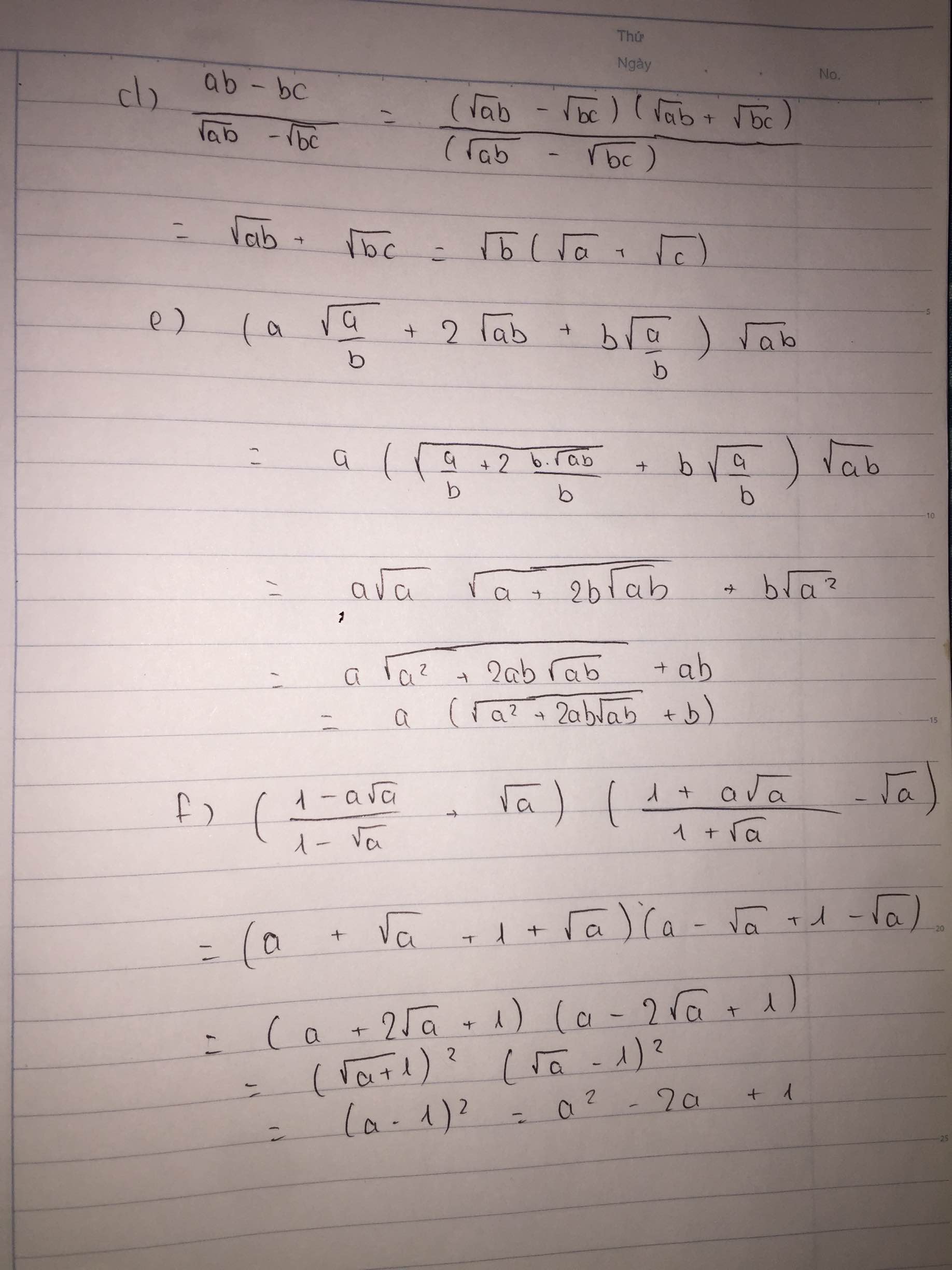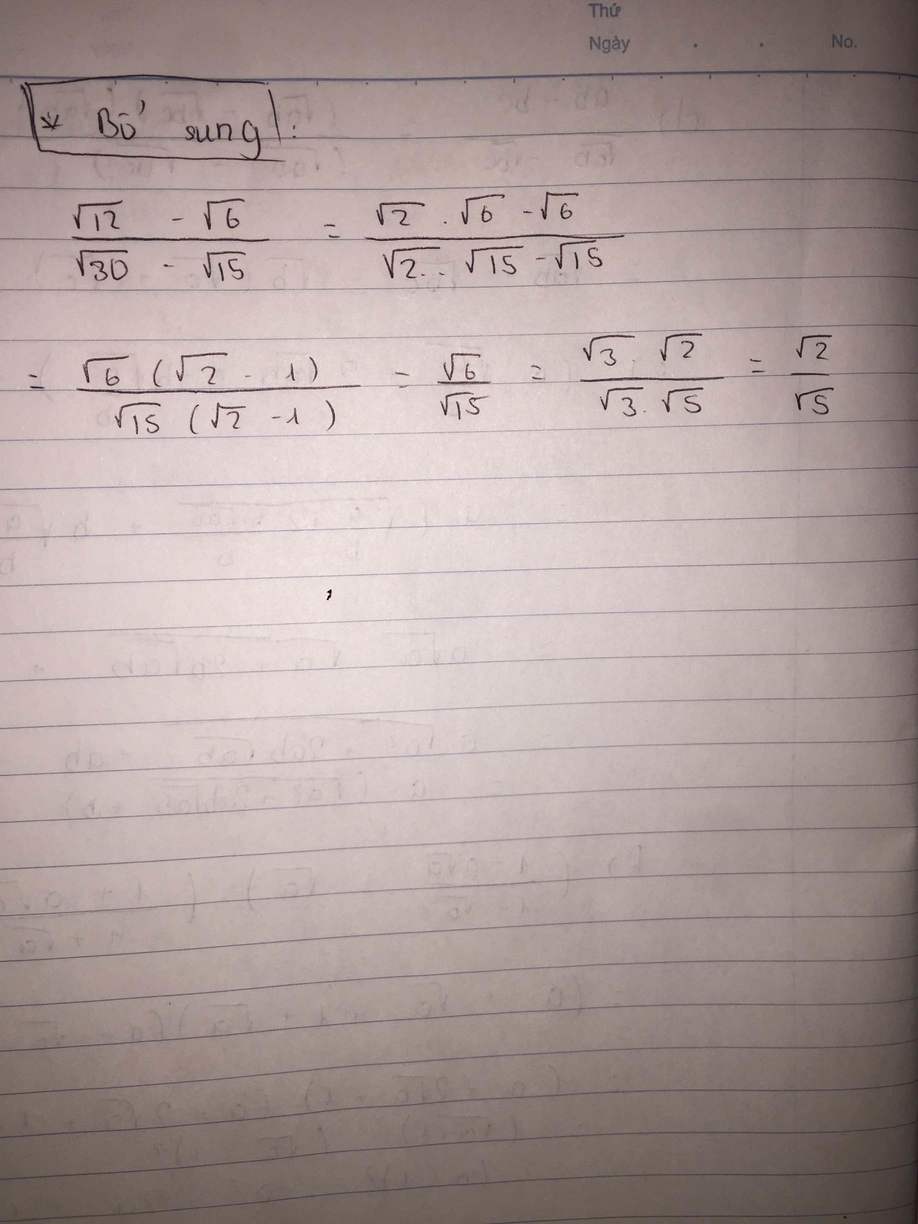Làm giúp em câu F với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có KA là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AEKF có
\(\widehat{FAE}=\widehat{AFK}=\widehat{AEK}=90^0\)
Do đó: AEKF là hình chữ nhật
Suy ra: \(AK=EF\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(EF^2=AE\cdot AB\)
c: Ta có: \(AE\cdot AB+AF\cdot AC+KB\cdot KC\)
\(=AH^2+AH^2+AH^2\)
\(=3\cdot EF^2\)

Para 1 - b
Para 2 - a
Para 3 - c
T - F - T - T - NG
1 B
2 A
3 D
4 D
5 A

Câu 7:
a, \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
b, \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Theo PT: \(n_{Fe}=n_{H_2}=0,1\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,1.56}{10}.100\%=56\%\\\%m_{CuO}=44\%\end{matrix}\right.\)
c, \(n_{CuO}=\dfrac{10-0,1.56}{80}=0,055\left(mol\right)\)
Theo PT: \(n_{H_2SO_4}=n_{Fe}+n_{CuO}=0,155\left(mol\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{0,155.98}{100}.100\%=15,19\%\)
d, Theo PT: \(\left\{{}\begin{matrix}n_{FeSO_4}=n_{Fe}=0,1\left(mol\right)\\n_{CuSO_4}=n_{CuO}=0,055\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{FeSO_4}=0,1.152=15,2\left(g\right)\\m_{CuSO_4}=0,055.160=8,8\left(g\right)\end{matrix}\right.\)
Câu 8:
a, \(CuCO_3+2HCl\rightarrow CuCl_2+CO_2+H_2O\)
b, \(n_{CO_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
Theo PT: \(n_{CuCO_3}=n_{CO_2}=0,15\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CuCO_3}=\dfrac{0,15.124}{20}.100\%=93\%\\\%m_{CuCl_2}=7\%\end{matrix}\right.\)
c, \(n_{HCl}=2n_{CO_2}=0,3\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{0,3}{0,2}=1,5\left(M\right)\)


f: 5y^2-20=0
=>y^2-4=0
=>(y-2)(y+2)=0
=>y=2 hoặc y=-2
g: |x-2|-1=0
=>|x-2|=1
=>x-2=1 hoặc x-2=-1
=>x=3 hoặc x=1


\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB





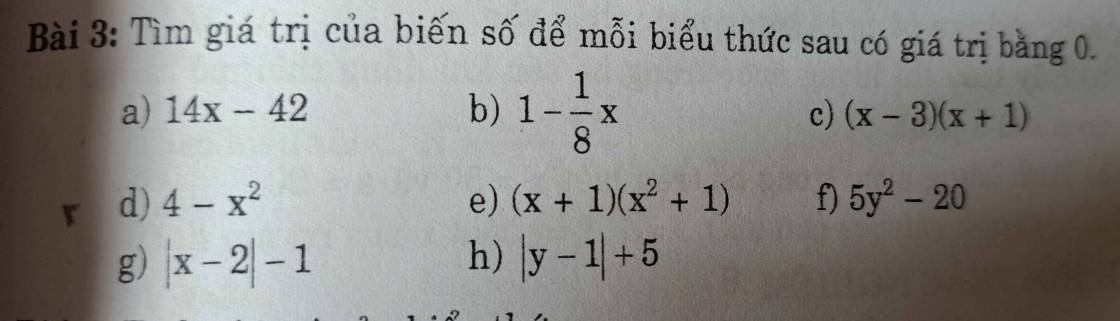
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.