cho d1: 3x+2y=13
d2:2x+3y=7
d3:x-y=6
d4:5x-0y=25
Hỏi 4đường thẳng trên có đồng quy không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


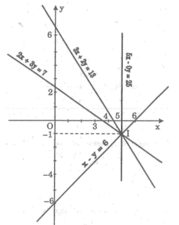
Ta có: ( d 3 ): x – y = 6 ⇔ y = x – 6
( d 4 ): 5x – 0y = 25 ⇔ x = 5
Vẽ đường thẳng ( d 3 ) là đồ thị hàm số y = x – 6
Cho x = 0 thì y = -6 ⇒ (0; -6)
Cho y = 0 thì x = 6 ⇒ (6; 0)
Vẽ đường thẳng ( d 4 ) là đường thẳng x = 5
Hai đường thẳng ( d 3 ) và ( d 4 ) cắt nhau tại I(5; -1). Lần lượt thay các giá trị x và y này vào phương trình đường thẳng ( d 1 ) và ( d 2 ), ta có:
( d 1 ): 3.5 + 2.(-1) = 15 – 2 = 13
( d 2 ): 2.5 + 3.(-1) = 10 – 3 = 7.
Vậy x và y thỏa mãn hai phương trình 3x + 2y = 13 và 2x + 3y = 7 nên (x; y) = (5; -1) là nghiệm của các phương trình trên. Hay là ( d 1 ) và ( d 2 ) đều đi qua I(5; -1).
Vậy bốn đường thẳng (d1): 3x + 2y = 13, ( d 2 ): 2x + 3y = 7, (d3): x – y = 6, (d4): 5x – 0y = 25 đồng quy.

Khó
a) d1 \(\ne\)d2\(\ne\)d3(1)
Giao d1 và d2 là : \(\int^{x+3y=1}_{2x-y=-5}\Leftrightarrow\int^{x=-2}_{y=1}\)(2)
Giao d1 và d3 là : \(\int^{x+3y=1}_{-3x+2y=8}\Leftrightarrow\int^{x=-2}_{y=1}\)(3)
(1)(2)(3) => dpcm
b) tương tự
hehehehehe mình cũng làm dc hahahahah

a, pt hoanh độ giao điểm cua 2 đg thẳng d1 và d2 la: 2x - 5 = 1 <=> x = 3
vậy tọa độ giao điểm cua d1 va d2 la A(3;1)
Để d1 , d2, d3 đồng quy thì d3 phải đi qua diem A(3;1)
Ta co pt: (2m - 3).3 - 1 = 1
<=> 6m - 9 -1 = 1
<=> 6m = 11 <=> m = 11/6
mấy bài còn lại tương tự nha

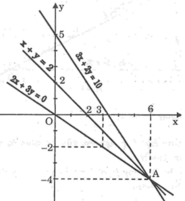
Vẽ đường thẳng ( d 1 ) là đồ thị hàm số y = -x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2 ⇒ (2; 0)
Vẽ đường thẳng (
d
2
) là đồ thị hàm số 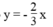
Cho x = 0 thì y = 0 ⇒ (0; 0)
Cho x = 3 thì y = -2 ⇒ (3; -2)
Hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại A(6; -4). Thay các giá trị x và y này vào phương trình đường thẳng ( d 3 ), ta có:
3.6 + 2.(-4) = 18 – 8 = 10.
Vậy x và y thỏa phương trình 3x + 2y = 10 nên (x; y) = (6; -4) là nghiệm của phương trình 3x + 2y = 10.

a, Hoành độ giao điểm d1 ; d2 thỏa mãn phương trình
\(3x+1=-x\Leftrightarrow4x+1=0\Leftrightarrow x=-\frac{1}{4}\)
\(\Rightarrow y=-\frac{3}{4}+1=\frac{1}{4}\)
Vậy d1 cắt d2 tại A(-1/4;1/4)
Để 3 điểm đồng quy khi d3 cắt A(-1/4;1/4) <=> \(\frac{1}{4}=-\frac{1}{4}+\frac{1}{2}\)( đúng )
Vậy 3 điểm đồng quy
b, d1 : \(y=1-x\)
Hoành độ giao điểm d1 ; d2 thỏa mãn phương trình
\(1-x=3x+5\Leftrightarrow4x=-4\Leftrightarrow x=-1\)
\(\Rightarrow y=-3+5=2\)
Vậy d1 cắt d2 tại T(-1;2)
Để 3 điểm đồng quy khi d3 cắt T(-1;2) <=> \(-1-\frac{2}{3}+\frac{5}{3}=0\)( luôn đúng )
Vậy 3 điểm đồng quy

Tọa độ giao điểm của đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=0\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Để 3 đường thẳng trên đồng qua thì:
\(\left(m^2-1\right)x+3y-5-2m=0\\ \Leftrightarrow\left(m^2-1\right).1+3.2-5-2m=0\\ \Leftrightarrow m^2-1+6-5-2m=0\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=x+2y-5\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=1\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
Thay x=1 và y=2 vào (d3), ta được:
\(m^2-1+3\cdot2-5-2m=0\)
\(\Leftrightarrow m\left(m-2\right)=0\)
hay \(m\in\left\{0;2\right\}\)

Cách giải
3 đthang đồng quy thì cắt nhau tại 1 điểm
Tìm giao điểm giữa d2 và d3
Nên ta phải giải hệ giữa d2 và d3 tìm được x,y
Nếu d1 đồng qui vs d2 và d3 thì nó phải đi qua giao điểm của d2 và d3. Ta thế x,y vào ptrinh d1 ta sẽ tìm được m.

Ba đường thẳng đã cho đồng quy khi hệ 2 x + 3 y = 1 x - y = 2 m x + ( 2 m + 1 ) y = 2 có nghiệm duy nhất.
Xét hệ gồm hai phương trình (1) và (2) :
2 x + 3 y = 1 ( 1 ) x - y = 2 ( 2 ) ⇔ 2 x + 3 y = 1 2 x - 2 y = 4 ⇔ 2 x + 3 y = 1 5 y = - 3 ⇔ x = 7 5 y = - 3 5
Hệ này có nghiệm duy nhất là 7 5 ; - 3 5 .
Để ba đường thẳng đã cho đồng quy thì 7 5 ; - 3 5 cũng là nghiệm của phương trình (3), tức là
m . 7 5 + 2 m + 1 . - 3 5 = 2 ⇔ 7 m - 3 2 m + 1 = 10 ⇔ 7 m - 6 m - 3 = 10 ⇔ m = 13 .