xy - x + y = -3
x^2 + y^2 - x + y + xy = 6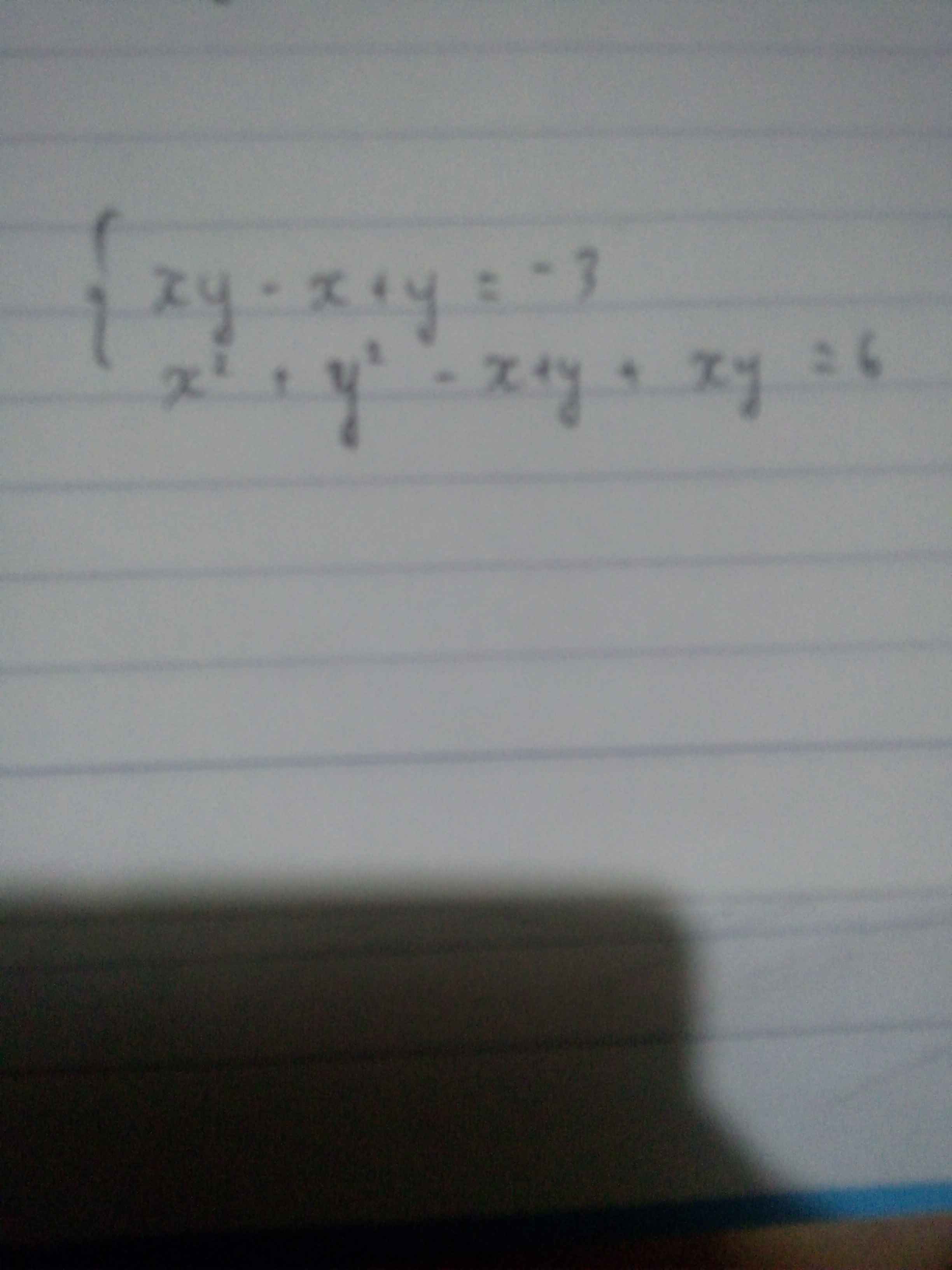
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2023
`a, (x-y)^2 = (x+y)^2 - 4xy = 12^2 - 35 . 4 = 144 - 140 = 4`.
`b, (x+y)^2 = (x-y)^2 + 4xy = 8^2 + 20.4 = 64 + 80 = 144`
`c, x^3 + y^3 = (x+y)^3 - 3xy(x+y) = 5^3 - 3 . 6 . 5 = 125 - 90 = 35`
`d, x^3 - y^3 = (x-y)^3 - 3xy(x-y) = 3^3 - 3 .40 . 3 = 27 - 360 = -333`.
24 tháng 11 2021
\(a,=\sqrt{x}\left(\sqrt{y}-\sqrt{x}\right)\\ b,=\left(\sqrt{x}-\sqrt{y}\right)^2\\ c,=\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)\\ d,=\sqrt{x}\left(\sqrt{y}+2\right)-3\left(\sqrt{y}+2\right)\\ =\left(\sqrt{x}-3\right)\left(\sqrt{y}+2\right)\)
T
4
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
a, x=1; y=2 => 12
x=2; y=1 => 21
b, x=1; y=5 => 15
x=5; y=1 => 51
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
c, x=1; y=6 => 16
x=6;y=1 => 61
x=2; y=3=> 23
x=3; y=2 => 32
d, x=1; y=8 => 18
x=2; y=4 => 24
x=4; y=2 => 42
x=8; y=1 => 81
CG
1
NM
Nguyễn Minh Quang
Giáo viên
12 tháng 8 2021
a. ta có : \(x^2+y^2=\left(x+y\right)^2-2xy=1^2-2\times\left(-6\right)=13\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=1^3-3\times\left(-6\right)\times1=19\)
\(x^5+y^5=\left(x+y\right)\left[x^4-x^3y+x^2y^2-xy^3+y^4\right]\)
\(=\left(x+y\right)\left[\left(x^2+y^2\right)^2-x^2y^2-xy\left(x^2+y^2\right)\right]=1.\left(13^2-\left(-6\right)^2-\left(-6\right).13\right)=211\)
b.\(x^2+y^2=\left(x-y\right)^2+2xy=1+2\times6=13\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)=1^3+6.3.1=19\)
\(x^5-y^5=\left(x-y\right)\left[\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)\right]\)
\(=\left(x-y\right)\left[\left(x^2+y^2\right)^2-x^2y^2+xy\left(x^2+y^2\right)\right]=1.\left(13^2-6^2+6.13\right)=211\)
24 tháng 9 2022
a: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{3}=\dfrac{13}{6}\sqrt{6}-2\sqrt{3}\)
b: \(VT=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\cdot\left(\sqrt{x}+\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)^2\)
c: \(VT=\dfrac{\sqrt{y}}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{\sqrt{x}}{\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)}\)
\(=\dfrac{y-x}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{-\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)
NT
0
14 tháng 10 2021
\(A,VT=x^3+y^3+x^3-y^3=2x^3=VP\\ B,VT=\left(x-y\right)\left(x^2+xy+y^2\right)=\left(x-y\right)\left(x^2+2xy+y^2-xy\right)\\ =\left(x-y\right)\left[\left(x+y\right)^2-xy\right]=VP\)
Sửa câu b \(cm:x^3-y^3=\left(x-y\right)\left[\left(x+y\right)^2-xy\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}3xy-3\left(x-y\right)=-9\\x^2+y^2+xy-\left(x-y\right)=6\end{matrix}\right.\)
Trừ vế cho vế:
\(x^2+y^2-2xy+2\left(x-y\right)=15\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)-15=0\Rightarrow\left[{}\begin{matrix}x-y=3\\x-y=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=x-3\\y=x+5\end{matrix}\right.\)
Thế vào pt đầu:
\(\Rightarrow\left[{}\begin{matrix}x\left(x-3\right)-x+x-3=-3\\x\left(x+5\right)-x+x+5=-3\end{matrix}\right.\)
\(\Leftrightarrow...\)