Cho 2 hàm số\(\text{ y=(m-3)x+3}\) và \(\text{y=\dfrac{3}{2}x-m}\) có đồ thị lần lượt là (d) và (d'); trong đó m là tham số.
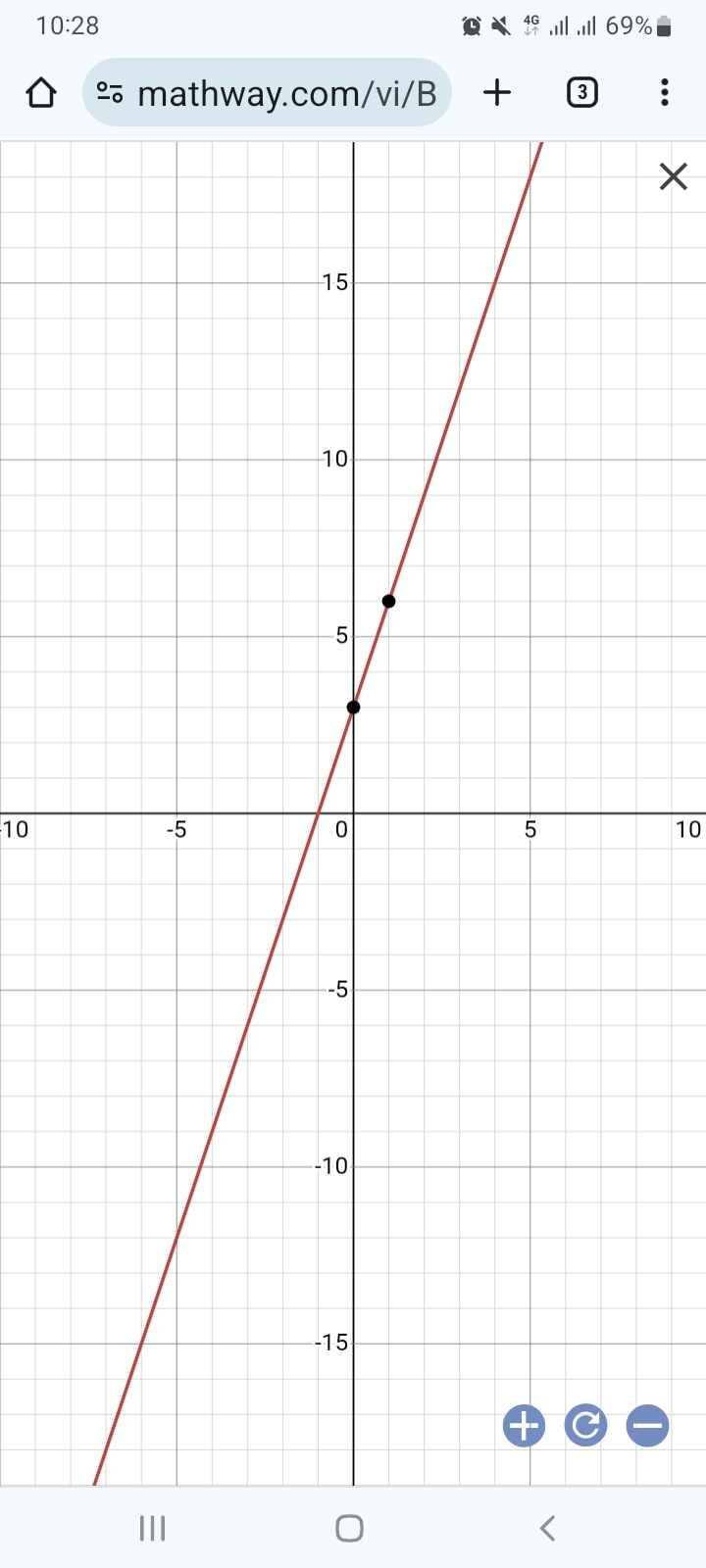
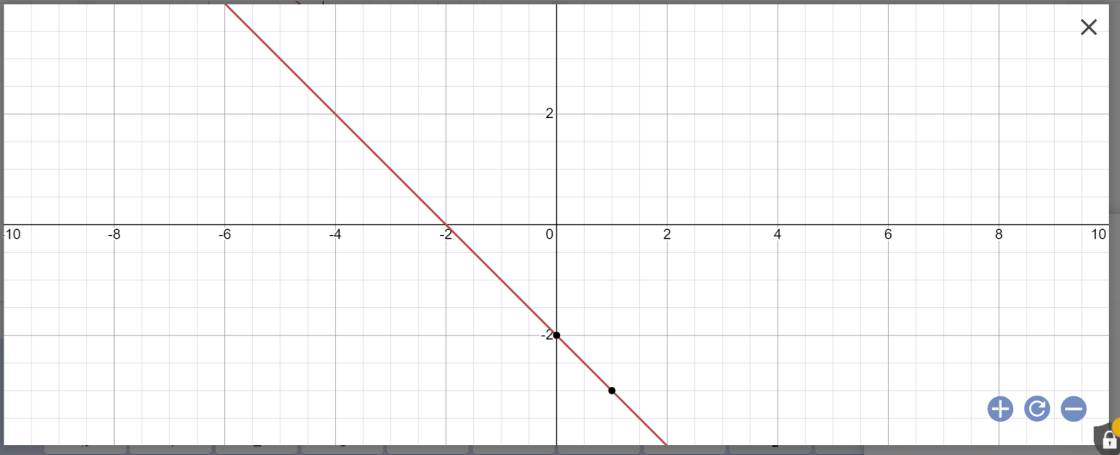
a) Khi (d) và (d') cùng đi qua 1 điểm có hoành độ =2, hãy tìm m và vẽ (d), (d') ứng với m vừa tìm.
b) Tìm m để (d) song song với đường thẳng (d1): y=2x+m
c) Tìm m để (d') vuông góc với đường thẳng (d2): y=mx

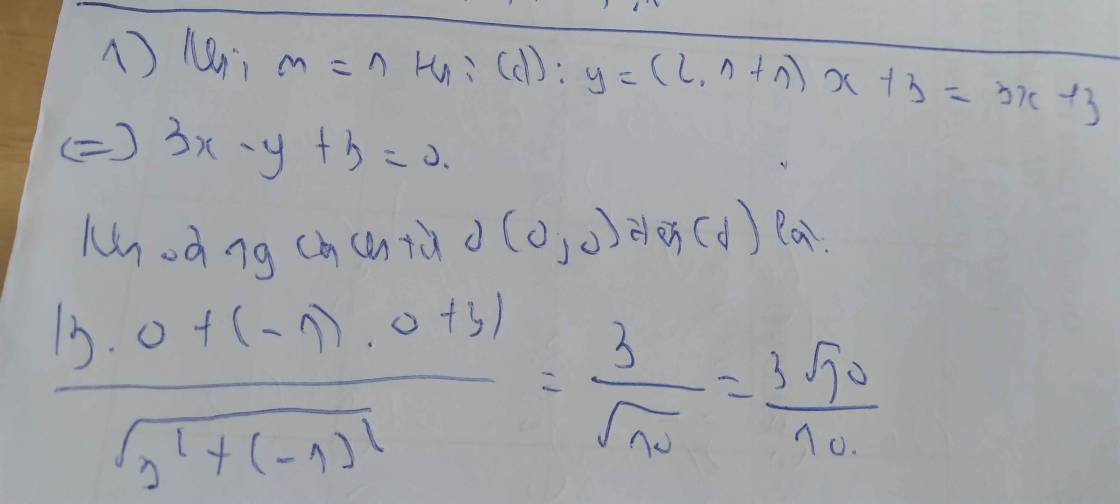



b: Để (d) vuông góc với (d1) thì \(2\left(m-3\right)=-1\)
\(\Leftrightarrow m-3=-\dfrac{1}{2}\)
hay \(m=\dfrac{5}{2}\)