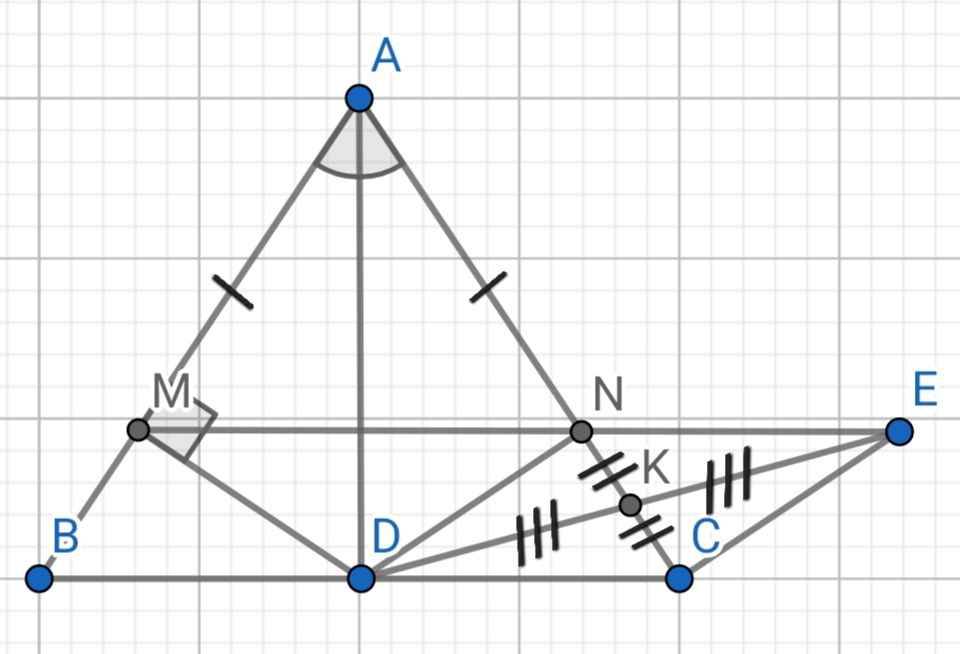
Cho tam giác ABC có AB=AC. Tia phân giác Am của góc BAC cắt BC tại D .Gọi H, K tương ứng là hình chiếu của D xuống AB,AC.
1, CM AD vuông góc với BC và D là trung điểm của cạnh BC
2, CM DH=DK và AD là đường trung trực của đoạn thẳng HK
3, Giả sử góc BAC =4góc B.Tính ^ BAD