Cho hàm số y=(K-3)x+K' (d) Tìm giá trị của K, K' sao cho (d) cắt 2 điểm A(1;2) và B(-3;4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 2 2018
Để biểu thức ở vế phải xác định thì k ≥ 0.
k + 3 = 2 3 ⇔ k = 3 ⇒ k = 3.
CM
6 tháng 7 2019
Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 1 khi:
Vậy đường thẳng (d) không cắt trục hoành tại điểm có hoành độ bằng 1 với mọi giá trị của k ≥ 0.
Nói các khác, đường thẳng y = k + 1 3 - 1 . x + k + 3 không bao giờ cắt trục hoành tại điểm có hoành độ bằng 1.
17 tháng 8 2021
a: Vì \(\left(d\right)\) đi qua \(A\left(1;2\right);B\left(-3;4\right)\) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}k+k'-3=2\\-3\left(k-3\right)+k'=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k+k'=5\\-3k+k'=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4k=10\\k+k'=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=\dfrac{2}{5}\\k'=\dfrac{23}{5}\end{matrix}\right.\)
9 tháng 5 2017
Đk: \(k\ge0\)
a)
A(0,2\(\sqrt{3}\))
x=0
\(\Rightarrow y=\sqrt{k}+\sqrt{3}\)
\(\Rightarrow\sqrt{k}=2\sqrt{3}-\sqrt{3}=\sqrt{3}\)
\(\Rightarrow k=3\) nhận
b)
\(B\left(1;0\right)\)
\(\Leftrightarrow\dfrac{\sqrt{k}+1}{\sqrt{3}-1}.1+\sqrt{k}+\sqrt{3}=0\)
\(\Leftrightarrow\sqrt{k}+1+\sqrt{k}.\left(\sqrt{3}-1\right)+\sqrt{3}\left(\sqrt{3}-1\right)=0\)
\(\Leftrightarrow\sqrt{3}\sqrt{k}+4-\sqrt{3}=0\)
\(4>\sqrt{3}\Rightarrow Vo..N_0\)
(d) không đi qua điểm B(1;0)
c) Sửa đề \(k\ge0\)
\(\Leftrightarrow y=\dfrac{\sqrt{k}.x+x+\sqrt{3}\sqrt{k}-\sqrt{k}+\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Leftrightarrow y=\dfrac{\sqrt{k}\left(x+\sqrt{3}-1\right)+x+\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
Với \(x=1-\sqrt{3}\) => y=\(\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{3}-1\) không phụ thuộc k
Điểm cố định
D\(\left(\left(1-\sqrt{3}\right);\left(\sqrt{3}+1\right)\right)\)
AH
Akai Haruma
Giáo viên
4 tháng 1 2024
Lời giải:
** Sửa lại hàm số: $y=-x+3$
a. Bạn có thể tự vẽ.
b. Để $y=(2k-1)x+1$ song song với (d)$ thì:
$2k-1=-1$
$\Leftrightarrow k=0$
c. PT hoành độ giao điểm của $(d)$ và $y=(k-3)x+5$:
$-x+3=(k-3)x+5$
$\Leftrightarrow (k-2)x=-2$
$\Leftrightarrow x=\frac{-2}{k-2}$ (đk: $k\neq 2$)
Khi đó: $y=-x+3=\frac{2}{k-2}+3$
Hai đths cắt nhau tại điểm có tung độ $7$
$\Leftrightarrow \frac{2}{k-2}+3=7$
$\Leftrightarrow \frac{2}{k-2}=4$
$\Leftrightarrow k-2=\frac{1}{2}\Leftrightarrow k=2,5$
4 tháng 1 2024
a: Sửa đề: y=-x+3
Vẽ đồ thị
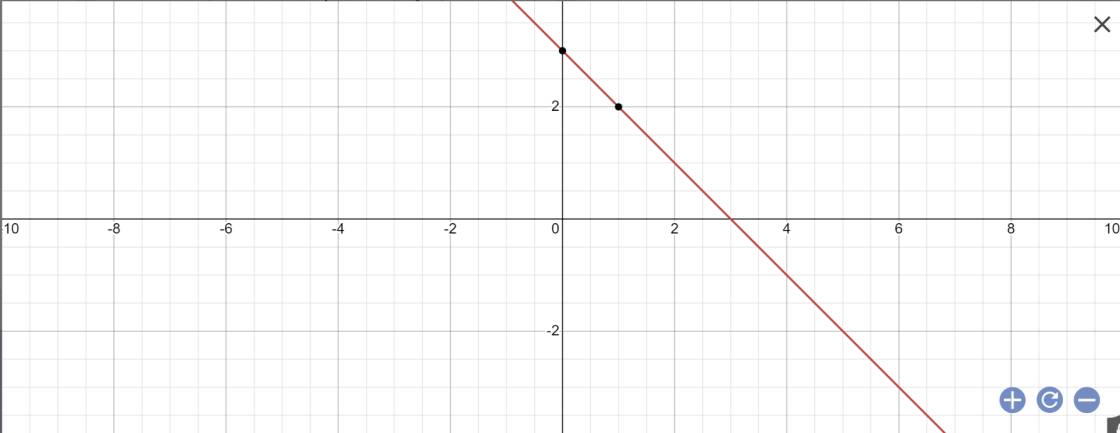
b: Để đường thẳng y=(2k-1)x+1 song song với (d) thì
\(\left\{{}\begin{matrix}2k-1=-1\\1\ne3\left(đúng\right)\end{matrix}\right.\)
=>2k-1=-1
=>2k=0
=>k=0
c: Thay y=7 vào y=-x+3, ta được:
-x+3=7
=>-x=4
=>x=-2
Thay x=-2 và y=7 vào y=(k-3)x+5, ta được:
-2(k-3)+5=7
=>-2(k-3)=2
=>k-3=-1
=>k=2
14 tháng 8 2021
a: Thay x=0 và y=0 vào \(\left(d\right)\), ta được:
k=0
13 tháng 12 2023
a: Tọa độ A là;
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
Vậy: A(3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+3=-0+3=3\end{matrix}\right.\)
Vậy: B(0;3)
O(0;0); A(3;0); B(0;3)
\(OA=\sqrt{\left(3-0\right)^2+\left(0-0\right)^2}=3\)
\(OB=\sqrt{\left(0-0\right)^2+\left(3-0\right)^2}=\sqrt{0^2+3^2}=3\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{9}{2}\)
b:
Để (d1) cắt (d2) thì k+1<>-1
=>k<>-2
Phương trình hoành độ giao điểm là:
(k+1)x+1=-x+3
=>(k+1)x+x=2
=>x(k+2)=2
=>\(x=\dfrac{2}{k+2}\)
Để hoành độ là số nguyên nhỏ nhất thì \(\dfrac{2}{k+2}\) là số nguyên nhỏ nhất có thể
=>k+2=-1
=>k=-3
CM
11 tháng 8 2019
Chọn D.
Phương trình đường thẳng d có hệ số góc k và đi qua I(1; 2) là d: y = k(x - 1) + 2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
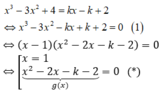
Để d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x1; x2 khác 1.
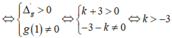
Hơn nữa theo Viet ta có
nên I là trung điểm AB.
Vậy chọn k > -3, hay k ∈ (-3;+∞).