1. Trong hệ trục Oxy cho: A(1;-2), B(-3;3)
Tìm điểm C (m; -2-m) sao cho tam giác ABC vuông tại C.
2. A(-3;4), B(1;1), C(9;-5)
a, CMR A, B, C thẳng hàng
b, Tìm E ∈ Ox : A, B, E thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Gọi tọa độ điểm P ( x; y )
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PA}=\left(1-x;4-y\right)\\\overrightarrow{PB}=\left(6-x;-1-y\right)\end{matrix}\right.\)
Mà \(\overrightarrow{PA}=\dfrac{1}{3}\overrightarrow{PB}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=\dfrac{1}{3}\left(6-x\right)\\4-y=\dfrac{1}{3}\left(-1-y\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=\dfrac{13}{2}\end{matrix}\right.\)
Vậy tọa độ của điểm P thỏa mãn là : \(P\left(-\dfrac{3}{2};\dfrac{13}{2}\right)\)

a: d'//d
=>d': 3x-y+c=0
Thay x=3 và y=-2 vào (d'), ta được:
c+9+2=0
=>c=-11
b: x=6+21t và y=1-3t
=>(d2) đi qua A(6;1) và có VTCP là (21;-3)=(7;-1)
=>VTPT là (1;7)
M(4;-14)
Phương trình (d2) là:
1(x-6)+7(y-1)=0
=>x-6+7y-7=0
=>x+7y-13=0
=>(d3): x+7y+c=0
Thay x=4 và y=-14 vào (d3),ta được:
c+4-98=0
=>c=94
trong hệ trục tọa độ oxy cho A(1;2) B(-1;1) C(5;-1) tìm M sao cho |vectoMA + vectoMB + vectoMC | min


Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 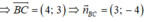
(BC): 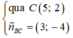
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
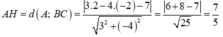

a) y = -3/4 x + 1/2
a = -3/4
b) d1 //d => m2 -1 =-3/4 và m khác 1/2
=> m2 = 1/4 => m =1/2 (loại)
m = -1/2 (TM)
Vậy m =-1/2

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;3\right)\\\overrightarrow{AC}=\left(-3;5\right)\\\overrightarrow{BC}=\left(-1;2\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{13}\\AC=\sqrt{34}\\BC=\sqrt{5}\end{matrix}\right.\)
\(cos\widehat{BAC}=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{21}{\sqrt{442}}\)
\(\Rightarrow\widehat{BAC}\approx2^043'\)

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
1)
\(\overrightarrow{CA}=\left(1-m;m\right)\\ \overrightarrow{CB}=\left(-3-m;m+5\right)\)
Tam giác ABC vuông tại C\(\Rightarrow\overrightarrow{CA}.\overrightarrow{CB}=\overrightarrow{0}\Leftrightarrow\left(m-1\right)\left(m+3\right)+m\left(m+5\right)=0\)
Tìm m rồi thay vào C
2) \(\overrightarrow{AB}=\left(4;-3\right),\overrightarrow{AC}=\left(12;-9\right)\Rightarrow\overrightarrow{AC}=3\overrightarrow{AB}\Rightarrow\)A,B,C thẳng hàng
b)\(E\left(x;0\right)\)
\(\overrightarrow{AE}=\left(x+3;-4\right)\)
A, B, E thẳng hàng \(\Leftrightarrow4.\left(-4\right)=-3\left(x+3\right)\Leftrightarrow x=\dfrac{7}{3}\)
Vậy \(E\left(\dfrac{7}{3};0\right)\)