Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E.
a) Chứng minh: EA.EB = ED.EC và góc EAD = góc ECB
b) Cho góc BMC = 1200 và SAED = 36 cm2. Tính SECB?
c) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD + CM.CA có giá trị không đổi.
d) Kẻ DH ⊥ BC (H∈ BC). Gọi P, Q lần lượt là trung điểm của các đoạn thẳng BH, DH. Chứng minh CQ ⊥ PD.
Các bạn làm ơn giải chi tiết giúp mình ! Thanks



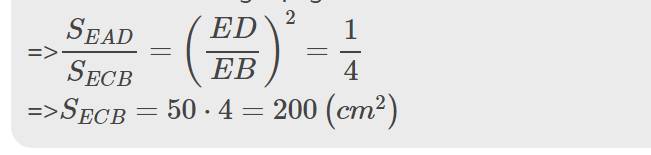
a: Xét ΔEAC vuông tại A và ΔEDB vuông tại D có
góc E chung
Do đó: ΔEAC đồng dạng với ΔEDB
=>EA/ED=EC/EB
hay \(EA\cdot EB=EC\cdot ED\)
=>EA/EC=ED/EB
=>ΔEAD đồng dạng với ΔECB
=>góc EAD=góc ECB
b: góc MBC+góc MCB=180-120=60 độ
=>90 độ-góc ECB+90 độ-góc CBE=60 độ
=>góc ECB+góc CBE=180 độ-60 độ=120 độ
=>góc E=60 độ
ΔEAD đồng dạng với ΔECB nên \(\dfrac{S_{EAD}}{S_{ECB}}=\left(\dfrac{EA}{EC}\right)^2=cos^260^0=\dfrac{1}{4}\)
=>\(S_{ECB}=144\left(cm^2\right)\)