Cho biết tổng :12+22+32+...+n2=a. Hãy tính 22+42+62+...+(2n)2theo giá trị của a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
ND
1

11 tháng 3 2021
Ta có \(2^2+4^2+...+20^2=2^2\left(1^2+2^2+...+10^2\right)=2^2.385=1540\).

CM
16 tháng 7 2018
S = 22 + 42 + 62 + ... + 202
= (2.1)2 + (2.2)2 + (2.3)2 ... (2.10)2
= 22.12 + 22.22 + 22.32 + ... + 22.102
= 22 (12 + 22 + ... + 102 )
= 4 . 385 = 1540

16 tháng 9 2017
Ta có : \(1^2+2^2+3^2+.....+10^2=385\)
\(\Leftrightarrow2^2\left(1^2+2^2+3^2+.....+10^2\right)=2^2.385\)
\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=4.385\)
\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=1540\)

AH
Akai Haruma
Giáo viên
2 tháng 1 2021
Lời giải:
\(B=(1.2)^2+(2.2)^2+(3.2)^2+...+(10.2)^2\)
\(=2^2.1^2+2^2.2^2+2^2.3^2+...+2^2.10^2=2^2(1^2+2^2+...+10^2)\)
\(=4A=4.385=1540\)
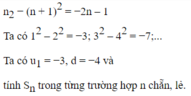

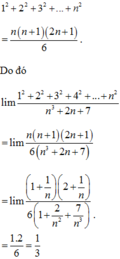

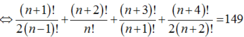
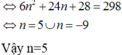
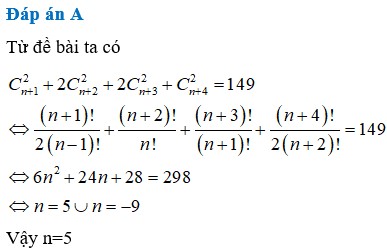
\(2^2+4^2+...+\left(2n\right)^2=1^2.2^2+2^2.2^2+....+n^2.2^2\)
\(2^2.\left(1^2+2^2+....+n^2\right)=2^2.n=4n\)
\(=>2^2+4^2+...+\left(2n\right)^2=4n\)
\(2^2+4^2+6^2+....+\left(2n\right)^2\)
\(=\left(1\cdot2\right)^2+\left(2\cdot2\right)^2+\left(2\cdot3\right)^2+....+\left(2n\right)^2\)
\(=1^2\cdot2^2+2^2\cdot2^2+2^2\cdot3^2+.....+2^2\cdot n^2\)
\(=2^2.\left(1^2+2^2+3^2+....+n^2\right)\)
\(=2^2a=4a\)