trên 1 đường thẳng lấy n điểm A1; A2; ........; An.Chia các điểm này vẽ các đường thẳng song song với nhau . Tính n để trong hình có 100 tia.
Mai mk cần rùi, cô giáo mà kiểm tra vào trúng mk mà ko lm là tèo lun, nên jup mk nha!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

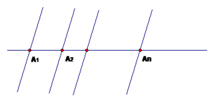
Tại mỗi điểm A1, A2,....,An đều có 4 tia.
Do đó để trong hình có 100 tia thì n = 100 : 4 = 25 (điểm)

Bổ sung giả thiết là \(n\) điểm đó nằm trên \(xy\)
Số các tia có gốc O là \(n\).
Ta nhận thấy số các tia có gốc là các điểm \(A_i\left(1\le i\le n\right)\) chính là \(A^2_n=\dfrac{n!}{\left(n-2\right)!}=n\left(n-1\right)=n^2-n\)
Từ đề bài, ta suy ra \(n^2-n+n=40\Leftrightarrow n^2=40\), vô lí.
(Mình nghĩ đề bài là 49 tia thì khi đó \(n=7\))