\(\overrightarrow{\frac{31x32-62}{30x1}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



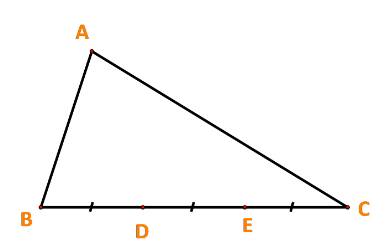
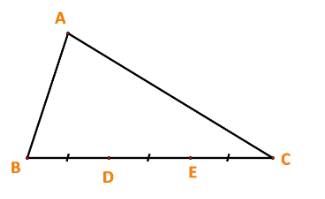
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a \)
Lại có: vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )\)
Tương tự: vecto \(\overrightarrow {BE} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )\)
Ta có:
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)



\(\frac{1}{20}\cdot\frac{1}{30}\cdot\frac{1}{42}\cdot\frac{1}{56}\cdot\frac{1}{72}\cdot\frac{1}{90}\)
\(=\frac{1}{4\cdot5}+\frac{1}{5\cdot6}+\frac{1}{6\cdot7}+\frac{1}{7\cdot8}+\frac{1}{8\cdot9}+\frac{1}{9\cdot10}\)
\(=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}\)
\(=\frac{1}{4}-\frac{1}{10}\)
\(=\frac{6}{40}=\frac{3}{20}\)

\(\overrightarrow{BI}=\overrightarrow{BC}+\overrightarrow{CI}=\overrightarrow{BC}-\frac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{BG}=\frac{1}{3}\left(\overrightarrow{BI}+\overrightarrow{BC}\right)=\frac{1}{3}\left(\overrightarrow{BC}-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}\right)=\frac{2}{3}\overrightarrow{BC}-\frac{1}{6}\overrightarrow{AB}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}-\frac{1}{6}\overrightarrow{AB}=\frac{5}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}=\frac{5}{6}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}\)

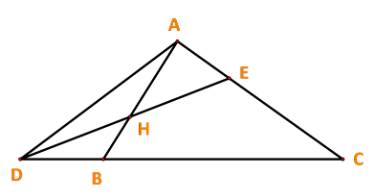
Dễ thấy: \(\overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {AC} = - \overrightarrow {AB} + \overrightarrow {AC} \)
Ta có:
+) \(\overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BD} \). Mà \(\overrightarrow {BD} = - \overrightarrow {DB} = - \frac{1}{3}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {AB} + \left( { - \frac{1}{3}} \right)( - \overrightarrow {AB} + \overrightarrow {AC} ) = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
+) \(\overrightarrow {DH} = \overrightarrow {DA} + \overrightarrow {AH} = - \overrightarrow {AD} + \overrightarrow {AH} \).
Mà \(\overrightarrow {AD} = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} ;\;\;\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} .\)
\( \Rightarrow \overrightarrow {DH} = - \left( {\frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} } \right) + \frac{2}{3}\overrightarrow {AB} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\)
+) \(\overrightarrow {HE} = \overrightarrow {HA} + \overrightarrow {AE} = - \overrightarrow {AH} + \overrightarrow {AE} \)
Mà \(\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} ;\;\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {HE} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\)
b)
Theo câu a, ta có: \(\overrightarrow {DH} = \overrightarrow {HE} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \) Hai vecto \(\overrightarrow {DH} ,\overrightarrow {HE} \) cùng phương.
\( \Leftrightarrow \)D, E, H thẳng hàng