tìm các số a,b,c sao cho 4x4 + 81 chia hết cho ax2 + bx +c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Câu trả lời của alibaba nguyễn đúng mà hài!!!)
Sơ đồ Horner hoạt động như sau:
| 1 | 0 | a | b | c | |
| 3 | 1 | 3 | a+9 | 3a+b+27 | 9a+3b+c+27 |
| 3 | 1 | 6 | a+27 | 6a+b+108 | 27a+6b+c+351 |
| 3 | ... | ... | ... | ... | ... |
- Kẻ bảng, trên dòng đầu tiên ghi các hệ số của đa thức đầu tiên, ở đây là \(1,0,a,b,c\).
- Theo định lí Bezout thì đa thức sẽ có nghiệm bội 3 là số 3, do đó chừa một cột bên tay trái ghi nghiệm (là số 3).
- Hạ hệ số (là 1) xuống, thực hiện quy tắc "nhân ngang cộng chéo" (nhân từ nghiệm qua rồi cộng chéo lên).
- VD: 3 nhân 1 cộng 0 là 3, viết 3. 3 nhân 3 cộng a là a+9, viết a+9. 3 nhân (a+9) cộng b là 3a+b+27, viết 3a+b+27...
- Để 3 là nghiệm của đa thức thì hệ số cuối cùng là 0, tức là \(9a+3b+c+27=0\).
- Tự làm tiếp, ra thêm 2 cái phương trình nữa...

tham khảo
Vì P ( x ) = ax2ax2 + bx + c chia hết cho 5 với mọi giá trị nguyên của x nên :
P ( 0 ) ; P ( 1 ) ; P ( - 1 ) tất cả đều chia đều cho 5 .
Ta có :
P ( 0 ) chia hết cho 5
⇒ a . 02+ b . 0 + c chia hết cho 5
⇒ c chia hết cho 5
P ( 1 ) chia hết cho 5
⇒ a . 12 + b . 1 + c chia hết cho 5
⇒ a + b + c chia hết cho 5
Vì c chia hết cho 5 ⇒ a + b chia hết cho 5 ( 1 )
P ( - 1 ) chia hết cho 5
⇒ a . (−1)2(−1)2 + b . ( - 1 ) + c chia hết cho 5
⇒ a + b + c chia hết cho 5
Từ ( 1 ) ; ( 2 ) ⇒ a + b + a - b chia hết cho 5
⇒ 2a chia hết cho 5
Mà ƯCLN ( 2 ; 3 ) = 1 ⇒ a chia hết cho 5
Vì a + b chia hết cho 5 ; a chia hết cho 5 ⇒ b chia hết cho 5
Vậy a , b , c chia hết cho 5 . ( đpcm )

Câu hỏi của Phạm Hải Yến - Toán lớp 7 - Học toán với OnlineMath

Không biết đề có vấn đề không nữa, tại vì không có cách nào để rút được c ra hết do f(n+1)-f(n) kiểu gì c cũng bị khử. Tuy nhiên nếu xét trường hợp với mọi c thì thay n=3 trở lên giải ngược lại không có nghiệm c nào thỏa mãn hết hehe nên là mình nghĩ đề sẽ kiểu "với n=1 hoặc n=2" . Theo mình nghĩ là vậy...
Giả sử n=1 ta có:
\(f\left(1+1\right)-f\left(1\right)=1\Leftrightarrow f\left(2\right)-f\left(1\right)=1\Leftrightarrow4a+2b+c-a-b-c=1\Leftrightarrow3a+b=1\) (1)
Giả sử n=2 ta có:
\(f\left(2+1\right)-f\left(2\right)=4\Leftrightarrow f\left(3\right)-f\left(2\right)=4\Leftrightarrow9a+3b+c-4a-2b-c=4\Leftrightarrow5a+b=4\) (2)
Từ (1) và (2) ta có: \(\left\{{}\begin{matrix}3a+b=1\\5a+b=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=-\dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=\dfrac{3}{2}x^2-\dfrac{7}{2}x+c\) (với c là hằng số bất kì)

\(Q\left(0\right)=c⋮2014⋮1007\)
\(Q\left(1\right)=\left(a+b+c\right)⋮2014\Rightarrow\left(a+b\right)⋮2014\Rightarrow\left(2a+2b\right)⋮2014\)
\(Q\left(2\right)=\left(4a+2b+c\right)⋮2014\Rightarrow\left(4a+2b\right)⋮2014\)
\(\Rightarrow\left(4a+2b-2a-2b\right)⋮2014\)
\(\Rightarrow2a⋮2014\Rightarrow a⋮1007\Rightarrow b⋮1007\)
\(\Rightarrowđpcm\)



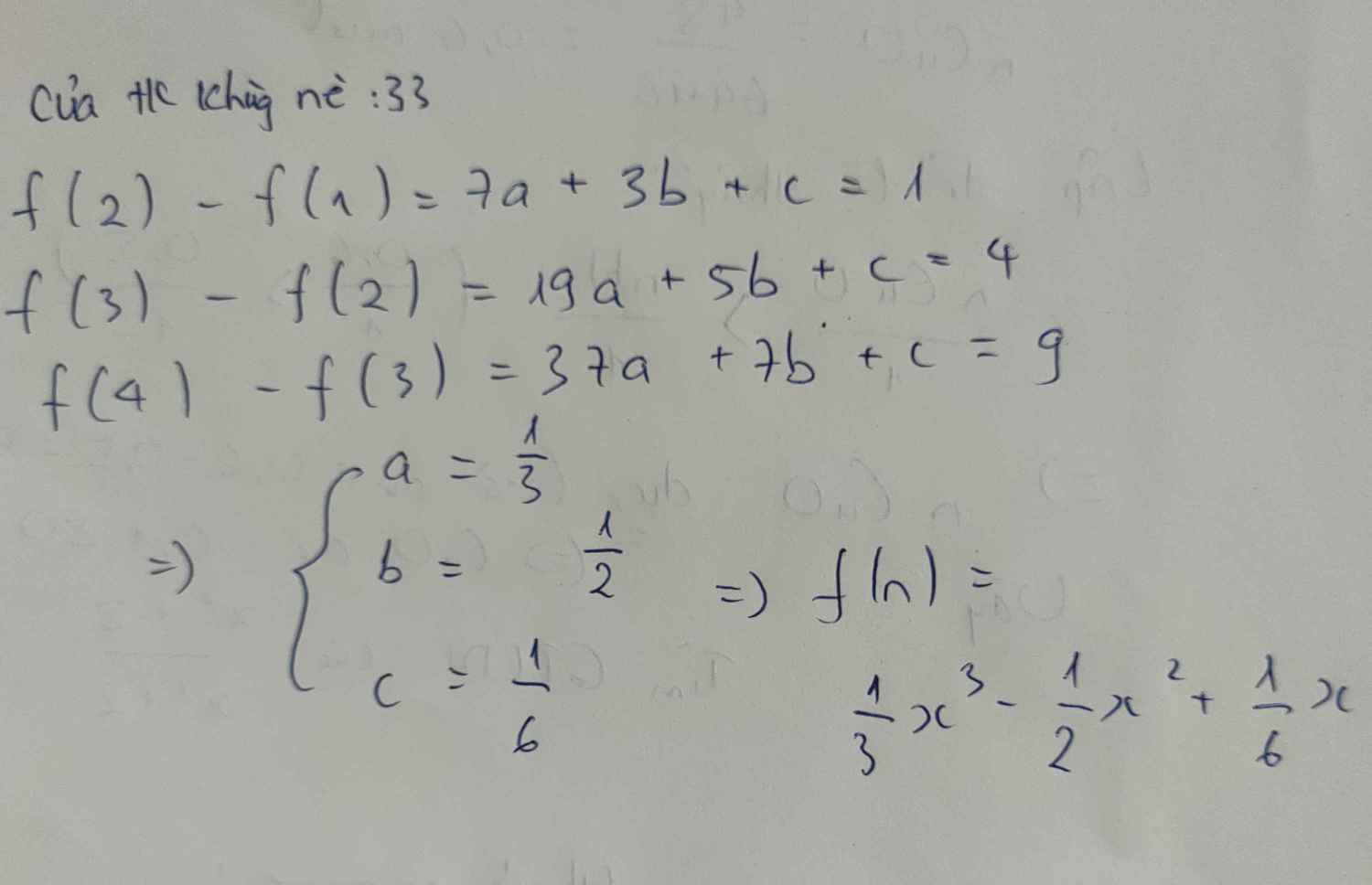
\(4x^4+81\)
\(=\left(2x^2\right)^2+2.2x^2.9+9^2-36x^2\)
\(=\left(2x^2+9\right)^2-\left(6x\right)^2\)
\(=\left(2x^2-6x+9\right)\left(2x^2+6x+9\right)\)
Vậy \(\orbr{\begin{cases}a=2,b=-6,c=9\\a=2,b=6,c=9\end{cases}}\)
Chúc bạn học tốt.
cảm ơn