a) Cho a+b=2. Tìm giá trị nhỏ nhất của A=a2 +b2
b) Cho x+2y=8. Tìm giá trị lớn nhất của B= xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$

Bài 2:
Ta có: M = a2+ab+b2 -3a-3b-3a-3b +2001
=> 2M = ( a2 + 2ab + b2) -4.(a+b) +4 + (a2 -2a+1)+(b2 -2b+1) + 3996
2M= ( a+b-2)2 + (a-1)2 +(b-1)2 + 3996
=> MinM = 1998 tại a=b=1
Câu 3:
Ta có: P= x2 +xy+y2 -3.(x+y) + 3
=> 2P = ( x2 + 2xy +y2) -4.(x+y) + 4 + (x2 -2x+1) +(y2 -2y+1)
2P = ( x+y-2)2 +(x-1)2+(y-1)2
=> MinP = 0 tại x=y=1

\(2x+y=6\Leftrightarrow x=\frac{6-y}{2}\)
a) \(A=2x^2+y^2=2\left(\frac{6-y}{2}\right)^2+y^2=\frac{2\left(6-y\right)^2}{4}+y^2\)
\(=\frac{2\left(36-12y+y^2\right)}{4}+y^2\)
\(=\frac{36-12y+y^2}{2}+\frac{2y^2}{2}=\frac{3y^2-12y+36}{2}\)
\(=\frac{3\left(y-2\right)^2+24}{2}\ge\frac{24}{2}=12\)(dấu "=" xảy ra khi y =2)
Vậy Min A = 12 khi y = 2
b) \(6=2x+y\ge2\sqrt{2xy}=2\sqrt{2B}\)
Suy ra \(8B\le36\Leftrightarrow B\le\frac{9}{2}\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}2x=y\\2x+y=6\end{cases}}\Leftrightarrow2x=y=3\Leftrightarrow\hept{\begin{cases}x=\frac{3}{2}\\y=3\end{cases}}\)
Vậy Max \(B=\frac{9}{2}\Leftrightarrow\hept{\begin{cases}x=\frac{3}{2}\\y=3\end{cases}}\)

a/ giá trị nhỏ nhất của A là 2
b/ giá trị lớn nhất của B là 51
tớ chỉ có bài tham khảo trên mạng thôi bạn thông cảm
Ta có: x + y = 1
<=> (x + y)3 = 1
<=> x3 + y3 + 3xy(x + y) = 1
<=> x3 + y3 + 3xy = 1 (do x + y = 1)
<=> x3 + y3 = 1 - 3xy
Áp dụng BĐT Cô - si, ta có:
xy >= (x+y)24=14(x+y)24=14
<=> -3xy≥−34≥−34
Ta có x3 + y3 = 1 - 3xy ≥1−34=14≥1−34=14
Dấu "=" xảy ra khi x = y = 1212
Vậy GTNN của x3 + y3 là 1414khi x = y = 12

Điều kiện x ≠ 2 và x ≠ 0
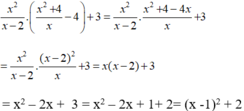
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

a)Giá trị nhỏ nhất của A là 2003
b)Giá trị lớn nhất của B là 9
Tick mình nha
a) \(a+b=2\)
=> \(b=2-a\)
\(A=a^2+\left(2-a\right)^2=2a^2-4a+4=\left(\sqrt{2}a-\sqrt{2}\right)^2+2\ge2\)
Vậy \(A_{min}=2\)
b) \(x+2y=8\)
=> \(x=8-2y\)
\(B=y\left(8-2y\right)=8y-2y^2=8-\left(\sqrt{2}y-2\sqrt{2}\right)^2\le8\)
Vậy \(B_{max}=8\)
a) \(\left(a-b\right)^2\ge0\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow2\left(a^2+b^2\right)\ge a^2+b^2+2ab\)
\(\Leftrightarrow a^2+b^2\ge\frac{\left(a+b\right)^2}{2}=\frac{2^2}{2}=2\)
Dấu \(=\)khi \(a=b=1\).
b) \(\left(x-2y\right)^2\ge0\Leftrightarrow x^2+4y^2\ge4xy\Leftrightarrow x^2+4xy+4y^2\ge8xy\)
\(\Leftrightarrow xy\le\frac{\left(x+2y\right)^2}{8}=\frac{8^2}{8}=8\)
Dấu \(=\)khi \(\hept{\begin{cases}x=4\\y=2\end{cases}}\).