Cho hình bình hành ABCD gọi d là đường thẳng đi qua A và ko cắt đoạn BD. Gọi BB',CC',DD' lần lượt là khoảng cách từ B,C,D đén đường thẳng d
Chứng minh BB'+CC'=DD'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
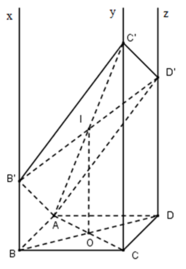
Trên Bx và Dz lấy điểm B′ và D′ sao cho BB’ = 2, DD’ =4
Gọi O là tâm hình bình hành ABCD, I là trung điểm của B′D′
Ta có BDD′B′ là hình thang, OI là đường trung bình của hình thang nên
OI // BB′ // DD′ // Cy
OI = B B ' + D D ' 2 = 2 + 4 2 = 3
Xét mặt phẳng tạo bởi OI và CC′ có: AI ∩ Cy = C′
Ta có OI // CC′, AO = OC suy ra AI = IC′
Suy ra OI là đường trung bình của tam giác ACC′ ⇒ CC′ = 2OI = 6
Đáp án cần chọn là: D

A B C D D' B' C' O d
- Gọi đường thẳng d cắt CD tại O
-Xét \(\Delta C'CO\)và \(\Delta B'BA\) , ta có :
+ \(\widehat{CC'O}=\widehat{BB'A}=90^o\)
+ \(\widehat{C'OC}=\widehat{B'AB}\)(2 góc ở vị trí so le trong )
=> \(\Delta C'CO~\Delta B'BA\left(g.g\right)\)
=> \(\frac{CC'}{CO}=\frac{BB'}{AB}\)
- Lại có :
- xét \(\Delta D'DO\)và \(\Delta C'CO\) ta có :
+ \(\widehat{DD'O}=\widehat{CC'O}=90^o\)
+ \(\widehat{D'OD}=\widehat{C'OC}\)( so le trong )
=> \(\Delta D'DO~\Delta C'CO\left(g.g\right)\)
=> \(\frac{DD'}{OD}=\frac{CC'}{OC}=\frac{CC'+DD'}{OD+OC}=\frac{CC'+DD'}{CD}=\frac{BB'}{AB}\)
MÀ AB = CD
nên ta có : CC' + DD' = BB'