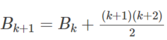hãy chứng minh đẳng thức sau:\(26^3-24^3>\left(26-24\right)^3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BL
5 tháng 7 2017
\(A=\dfrac{\left(5\sqrt{3}+5\sqrt{2}\right)\left(5-2\sqrt{6}\right)}{5\sqrt{3}-5\sqrt{2}}\\ =\dfrac{5\left(\sqrt{3}+\sqrt{2}\right)\left(3-2\sqrt{6}+2\right)}{5\left(\sqrt{3}-\sqrt{2}\right)}\\ =\dfrac{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)^2}{\sqrt{3}-\sqrt{2}}\\ =\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)\\ =3-2\\ =1\)
Vậy \(A=1\)
DD
2
14 tháng 11 2016
sssssssooooo sssssssaaaaaaaaannnnnnnnhhhhhhhhsssssss aaaaaaaaffffffff
15 tháng 10 2016
Ta có :
+ 26 mũ 3 - 24 mũ 3 = 3752
+ ( 26 - 24 ) mũ 3 = 8
Vì 3752 > 8
Nên 26 mũ 3 - 24 mũ 3 > (26 - 24 ) mũ 3
( Vì mk không biết cách đánh số mũ trên máy tính nên phải ghi như trreen .Mong bạn thông cảm nhé )
DL
2 tháng 10 2019
Áp dụng bất đẳng thức \(4x^3+4y^3\ge\left(x+y\right)^3\) với x, y > 0, ta được:
\(4a^3+4b^3\ge\left(a+b\right)^3\); \(4b^3+4c^3\ge\left(b+c\right)^3\) ; \(4c^3+4a^3\ge\left(c+a\right)^3\).
Cộng từng vế 3 bất đẳng thức trên ta được:
\(4a^3+4b^3+4a^3+4b^3+4c^3+4c^3\ge\left(a+b\right)^3+\left(c+b\right)^3+\left(a+c\right)^3\)
\(\Rightarrow8\left(a^3+b^3+c^3\right)\ge\left(a+b\right)^3+\left(c+b\right)^3+\left(a+c\right)^3\)
=> đpcm.
BT
0
CM
8 tháng 8 2018
Kiểm tra với n = 1
Giả sử đã cho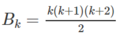 
Ta cần chứng minh
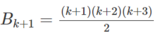
bằng cách tính
