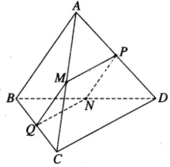
Cho tứ giác ABCD có P và Q lần lượt là trung điểm của AD và BC. Chứng minh rằng: 2PQ\(\le\)AB+CD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TB
Cho tứ giác ABCD có P và Q lần lượt là trung điểm của AD và BC. Chứng minh rằng: 2PQ \(\le\)AB + CD.
0

TB
0


CM
4 tháng 6 2019
Ta có:
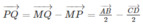
Do đó:
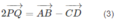
Mặt khác:
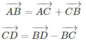
Nên
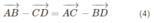
Vì 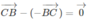
Từ (3) và (4) ta suy ra
![]()
là đẳng thức cần chứng minh.

31 tháng 8 2018
EF là đg trung bình ứng cạnh DC của tam giác ADC => EF= CD/2 tất nhiên < (AB+CD)/2
Gọi M là trung điểm của AC
Xét ΔADC có AP/AD=AM/AC
nên PM/DC=AP/AD=1/2
Xét ΔCAB có CM/CA=CQ/CB
nên MQ/AB=CQ/CB=1/2
PQ<=PM+MQ
=>PQ<=(AB+CD)/2
=>2PQ<=AB+CD