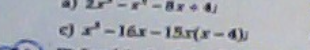\
mn giúp em câu này với ạ, đề là phân tích đa thứ thành nhân tử
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 8 2021
e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
5 tháng 8 2021
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)
20 tháng 8 2021
\(a^2x+a^2y+ax+ay+x+y\)
\(=a^2\left(x+y\right)+a\cdot\left(x+y\right)+\left(x+y\right)\)
\(=\left(x+y\right)\cdot\left(a^2+a+1\right)\)
26 tháng 7 2021
19. 3x2-4x+1
= 3x2-3x-x+1
= (3x2-3x)-(x-1)
= 3x(x-1)-(x-1)
= (3x-1)(x-1)
20.3x2+4x-7
= 3x2+3x-7x-7
= (3x2+3x)-(7x+7)
= 3x(x+1)-7(x-1)
= (3x-7)(x-1)
21.3x2+7x-6
= 3x2+9x-2x-6
= (3x2+9x)-(2x+6)
= 3x(x+3)-2(x+3)
= (3x-2)(x+3)
22.3x2+3x-6
= 3x2+6x-3x-6
=(3x2+6x)-(3x+6)
= 3x(x+2)-3(x+2)
=(3x-3)(x+2)
= 3(x-1)(x+2)
23. 3x2-3x-6
=(3x2-6x)+(3x-6)
=3x(x-2)+3(x-2)
=(3x+3)(x-2)
= 3(x+1)(x-2)
24.6x2-13x+6
= 6x2-9x-4x+6
= (6x2-9x)-(4x-6)
=3x(2x-3)-2(2x-3)
=(3x-2)(2x-3)
25.6x2+13x+6
= 6x2+9x+4x+6
= (6x2+9x)+(4x+6)
=3x(2x+3)+2(2x+3)
=(3x+2)(2x+3)
26. 6x2+15x+6
= (6x2+12x)+(3x+6)
= 6x(x+2)+3(x+2)
=(6x+3)(x+2)
=3(2x+1)(x+2)
27. 6x2-15x+6
= (6x2-12x)-(3x-6)
= 6x(x-2)-3(x-2)
=(6x-3)(x-2)
=3(2x-1)(x-2)
28. 6x2+20x+6
= (6x2+18x)+(2x+6)
= 6x(x+3)+2(x+3)
= (6x+2)(x+3)
= 2(3x+1)(x+3)
29.6x2-20x+6
= (6x2-18x)-(2x-6)
= 6x(x-3)+2(x-3)
= (6x-2)(x-3)
= 2(3x-1)(x-3)
30.6x2+12x+6
= (6x2+6x)+(6x+6)
= 6x(x+1)+6(x+1)
= (6x+6)(x+1)
= 6(x+1)(x+1)
= 6(x+1)2
5 tháng 8 2021
\(x\left(x-y\right)^2-y\left(x-y\right)^2+xy^2-x^2y\)
\(=\left(x-y\right)^2\left(x-y\right)-xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2-2xy+y^2-xy\right)\)
\(=\left(x-y\right)\left(x^2-3xy+y^2\right)\)
5 tháng 8 2021
2(x-y)2 -y(x-y)2 +xy2-x2y= 2(x-y)2-y(x-y)2+(xy^2-x^2y)=2(x-y)2-y(x-y)2+xy(x-y)=(x-y)\(\left[2\left(x-y\right)-y\left(x-y\right)+xy\right]\)=(x-y)(2x-2y-xy+y2+xy)=(x-y)(2x-2y+y2)
5 tháng 8 2021
\(2\left(x-y\right)^2-y\left(x-y\right)^2+xy^2-x^2y\)
\(=\left(x-y\right)^2\left(2-y\right)+xy\left(y-x\right)\)
\(=\left(x-y\right)^2\cdot\left(2-y\right)-xy\left(x-y\right)\)
\(=\left(x-y\right)\left[\left(x-y\right)\left(2-y\right)-xy\right]\)
BT
2
29 tháng 8 2023
o: x^4+x^3+x^2-1
=x^3(x+1)+(x-1)(x+1)
=(x+1)(x^3+x-1)
q: \(=\left(x^3-y^3\right)+xy\left(x-y\right)\)
=(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2
s: =(2xy)^2-(x^2+y^2-1)^2
=(2xy-x^2-y^2+1)(2xy+x^2+y^2-1)
=[1-(x^2-2xy+y^2]+[(x+y)^2-1]
=(1-x+y)(1+x-y)(x+y-1)(x+y+1)
u: =(x^2-y^2)-4(x+y)
=(x+y)(x-y)-4(x+y)
=(x+y)(x-y-4)
x: =(x^3-y^3)-(3x-3y)
=(x-y)(x^2+xy+y^2)-3(x-y)
=(x-y)(x^2+xy+y^2-3)
z: =3(x-y)+(x^2-2xy+y^2)
=3(x-y)+(x-y)^2
=(x-y)(x-y+3)
H9
HT.Phong (9A5)
CTVHS
29 tháng 8 2023
o) \(x^4+x^3+x^2-1\)
\(=\left(x^4+x^3\right)+\left(x^2-1\right)\)
\(=x^3\left(x+1\right)+\left(x+1\right)\left(x-1\right)\)
\(=\left(x+1\right)\left(x^3+x-1\right)\)
q) \(x^3+x^2y-xy^2-y^3\)
\(=\left(x^3+x^2y\right)-\left(xy^2+y^3\right)\)
\(=x^2\left(x+y\right)-y^2\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-y^2\right)\)
\(=\left(x+y\right)^2\left(x-y\right)\)
s) \(4x^2y^2-\left(x^2+y^2-1\right)^2\)
\(=\left(2xy\right)^2-\left(x^2+y^2-1\right)^2\)
\(=\left(2xy-x^2-y^2+1\right)\left(2xy+x^2+y^2-1\right)\)
\(=-\left(x^2-2xy+y^2-1\right)\left(x^2+2xy+y^2-1\right)\)
\(=-\left(x-y-1\right)\left(x-y+1\right)\left(x+y+1\right)\left(x+y-1\right)\)
u) \(x^2-y^2-4x-4y\)
\(=\left(x^2-y^2\right)-\left(4x+4y\right)\)
\(=\left(x+y\right)\left(x-y\right)-4\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-4\right)\)
x) \(x^3-y^3-3x+3y\)
\(=\left(x^3-y^3\right)-\left(3x-3y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-3\right)\)
z) \(3x-3y+x^2-2xy+y^2\)
\(=\left(3x-3y\right)+\left(x^2-2xy+y^2\right)\)
\(=3\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3+x-y\right)\)
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
Lời giải:
$y-x^2y-2xy^2-y^3=y(1-x^2-2xy-y^2)$
$=y[1-(x^2+2xy+y^2)]=y[1-(x+y)^2]=y(1-x-y)(1+x+y)$
20 tháng 8 2021
\(\left(x^2+2x\right)^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+4x^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+2x^2-4x-3=0\Leftrightarrow\left(x-1\right)\left(x+1\right)^2\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)
20 tháng 8 2021
Ta có: \(\left(x^2+2x\right)^2-2x^2-4x-3=0\)
\(\Leftrightarrow\left(x^2+2x\right)^2-2\left(x^2+2x\right)-3=0\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-3\\x=1\end{matrix}\right.\)
\(x^2-16x-15x\left(x-4\right)\)
\(=x\left(x-4\right)\left(x+4\right)-15x\left(x-4\right)\)
\(=\left(x-4\right)\left(x^2+4x-15x\right)\)
\(=\left(x-4\right)\left(x^2-11x\right)=x\left(x-4\right)\left(x-11\right)\)
\(=x\left(x-4\right)\left(x+4\right)-15x\left(x-4\right)\\ =x\left(x-4\right)\left(x-11\right)\)