Giúp em giải câu 11. 13 15 vs ăn
Giải thích dùm em luôn
Em cảm ơn 

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)

14.
\(y'=2x^3-4x=2x\left(x^2-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
\(y''=6x-4\)
\(\Rightarrow y''\left(0\right)=-4< 0\Rightarrow x=0\) là điểm cực đại
\(y\left(0\right)=-3\)
\(\Rightarrow\) Điểm cực đại của đồ thị hàm số là \(\left(0;-3\right)\)
12.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(y''=6x\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(1\right)=6>0\\y''\left(-1\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=-1\) là điểm cực đại
\(\Rightarrow\)Giá trị cực đại của hàm số là \(y\left(-1\right)=3\)

71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)

Câu 6:
a) a vuông góc với IJ
b vuông góc với IJ
=> a//b
b) KLJ + IKL = 180° ( 2 góc trong cùng phía)
75° + IKL = 180°
IKL = 180° - 75°
IKL = 105°

Gọi x là số mét tấm vải xanh ( x>18)
=> tấm vải đỏ = x - 18( mét) ( x> 18)
Sau khi cắt đi 1/2 tấm vải xanh và 1/5 tấm vải đỏ thì bằng nhau. Vậy, số tấm vải xanh còn lại là 1/2, số tấm vải đỏ còn lại là 4/5
=> ta có pt sau: \(\dfrac{x}{2}\)= \(\dfrac{4\left(x-18\right)}{5}\)
=> 5x = 8( x-18)
=> 5x = 8x - 144
=> - 3x = -144
=> 3x = 144
=> x = 48 ( thỏa)
=> tấm vải xanh dài 48m, tấm vải đỏ dài 30m
Đúng thì tim giúp mik nha. Thx bạn

1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:

Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
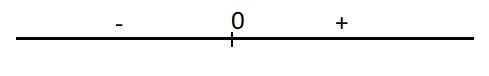
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)

(11+13+15+....+99)
có (99-11):2+1=45 (số hạng)
Tổng (99+11).45:2=2475
(10+12+14+...+98)
có (98-10):2+1=45(số hạng)
Tổng: (98+10).45:2=2430
(11+13+15+...+99) -(10+12+14+...+98)
= 2475 - 2430
= 45
Chúc học tốt :)
phép tính trên có số cặp là : (99 - 11) : 2 + 1= 45 (cặp)
(11 + 13 + 15 + ... + 97 + 99) - (10 + 12 + 14 + ... + 96 + 98)
= (11 - 10) + (13 - 12) + (15 - 14) + ... + (99 - 98)
= 1 + 1 + 1 + ... + 1 (có 45 số 1)
= 1x 45
= 45
vậy phép tính có kết quả là 45
t.i.c.k mình nha bạn ^^





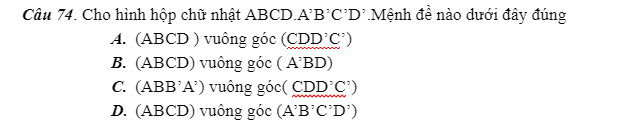
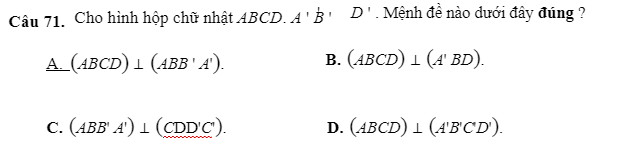

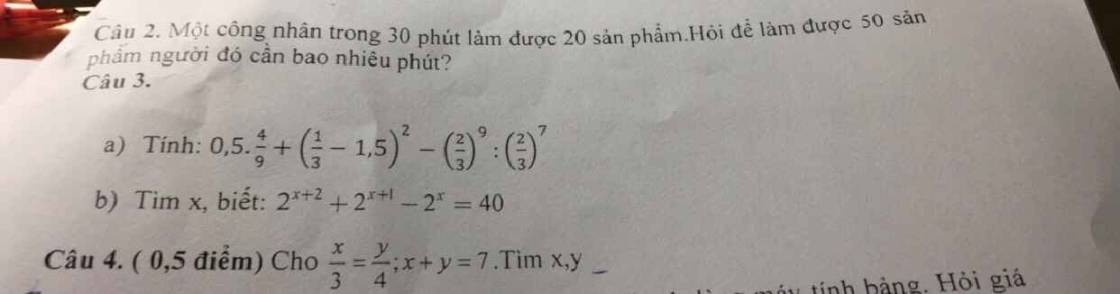 Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...
Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...



Đề mờ quá, bạn chụp lại được không