Cho tam giác ABC có điểm N thuộc cạnh AC ,M thuộc cạnh BC .Gọi I là giao điểm của AM và BN .hãy kể tên các bộ ba điểm , xác định điểm nằm giữa hai điểm còn lại trong mỗi trường hợp .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) M A B ^ = 70°.
b) Trong ba điểm N, M, C điểm M nằm giữa hai điểm còn lại
c) AM là tia phân giác của góc N A C ^ vì tia AM nằm giũa hai tia AN,AC và N A M ^ = M A C ^
a) Vì tia AM nằm giữa hai tia AB và AC, nên ta có:
ˆMAB+ˆMAC=ˆBACMAB^+MAC^=BAC^
⇒ˆMAB=ˆBAC−ˆMAC=90o−20o⇒MAB^=BAC^−MAC^=90o−20o
⇒ˆMAB=70o⇒MAB^=70o
b) Trong 3 điểm N, M, C điểm M nằm giữa hai điểm còn lại vì CM < CN.
c) Vì tia AN nằm giữa hai tia AB và AC, nên ta có:
ˆNAB+ˆNAC=ˆBACNAB^+NAC^=BAC^
⇒ˆNAC=ˆBAC−ˆNAB=90o−50o⇒NAC^=BAC^−NAB^=90o−50o
⇒ˆNAC=40o⇒NAC^=40o
Ta có AM nằm giữa hai tia AN và AC (1)
Và ˆCAM=ˆMAN=ˆNAC2=4002=20oCAM^=MAN^=NAC2^=4002=20o (2)
Từ (1) và (2) suy ra (đpcm)

a) M A B ^ = 70 °
b) Trong ba điểm N, M, C điểm M nằm giữa hai điểm còn lại
c) AM là tia phân giác của góc N A C ^ vì tia AM nằm giũa hai tia AN,AC và N A M ^ = M A C ^

Gọi D là đỉnh thức tư của hình bình hành ABDC. Khi đó, O, M, D thẳng hàng.
Do giả thiết nên DB//MP, DC//MN. Từ đó, do O, M, D thẳng hàng, nên góc PMO = góc OMN <=> OM là phân giác góc PMN <=> DM là phân giác góc BDC
\(\Leftrightarrow\frac{MB}{MC}=\frac{DB}{DC}\)
Nhưng tứ giác ABDC là một hình bình hành nên BD = AC, CD = AB
do đó : \(\frac{DB}{DC}=\frac{AC}{AB}\)
Vì vậy :
góc PMO bằng góc OMN \(\Leftrightarrow\frac{MB}{MC}=\frac{AC}{AB}\)
Vậy với M là điểm trên cạnh BC sao cho \(\frac{MB}{MC}=\frac{AC}{AB}\) (hay M đối xứng với chân phân giác trong góc BAC qua trung điểm cạnh BC) thì góc PMO bằng góc OMN => Điều cần chứng minh

a: Xét ΔBAMvà ΔBNM có
BA=BN
góc ABM=góc NBM
BM chung
=>ΔBAM=ΔBNM
=>MA=MN
b: Xét ΔBNK vuông tại N và ΔBAC vuông tại A có
BN=BA
góc NBK chung
=>ΔBNK=ΔBAC
=>BK=BC
Xét ΔMAK vuông tại A và ΔMNC vuông tại N có
MA=MN
góc AMK=góc NMC
=>ΔMAK=ΔMNC
=>MK=MC
=>BM là trung trực của CK
=>B,M,I thẳng hàng

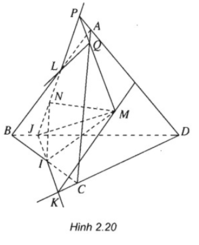
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
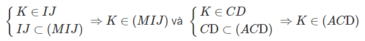
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
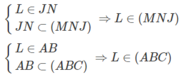
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
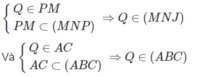
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).