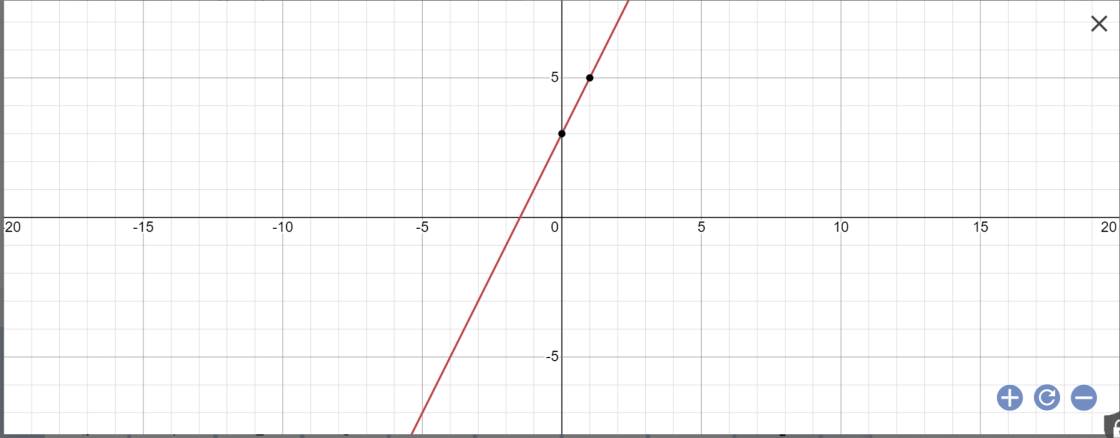
1) cho hàm số y=-2x+3 có đồ thị là (d)
A) vẽ đồ thị (d) của hàm số
B) đường thẳng (d) cắt trục hoành tại A và cắt trục tung tại B. Tính s tam giác A0B
2) tìm giá trị của m để 2 đt (d1): y=3x+m^2 và (d2):y= -2x +m +3 cắt nhau tại một điểm trên trục tung
Giúp mình phần 2 với ạ!